Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ABC và MN//BC
Hai tam giác AMN và ABC, có:
- góc AMN = góc ABC (đồng vị)
- góc ANM = góc ACB (đồng vị)
- BAC là góc chung
Mặt khác, theo hệ quả định lí Ta-lét, hai tam giác AMN và ABC có 3 cặp cạnh tương ứng tỉ lệ:
\(\frac{AM}{AB}=\frac{MN}{BC}=\frac{AN}{AC}\)
Nên tam giác AMN đồng dạng với tam giác ABC
\(\Rightarrow\frac{AM}{AB}=\frac{AN}{AC}=\frac{1}{3}\)
\(\Rightarrow\frac{AN}{18}=\frac{1}{3}\)
\(AN=\frac{18.1}{3}=6\)
Do AC = AN + NC
\(\Rightarrow NC=AC-AN=18-6=12\)
Vậy NC có độ dài là 12 cm

a: AN+CN=AC
=>AN=20-15=5cm
Xét ΔABC có AM/AB=AN/AC
nên MN//BC
b: Xét ΔAMN và ΔNPC có
góc AMN=góc NPC(=góc B)
góc ANM=góc NCP
=>ΔAMN đồng dạng với ΔNPC

M nằm giữa A và B nên: AB = AM + MB = 10cm
Theo định lí Ta let ta có:
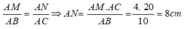
Chọn đáp án A

a) MN // BC. Áp dụng định lí Ta-let, ta có :
\(\frac{BM}{AB}=\frac{CN}{AC}\)hay \(\frac{2}{8}=\frac{CN}{10}\)\(\Rightarrow CN=2,5\)
b) MN // BP ; NP // BM nên tứ giác MNPB là hình bình hành
\(\Rightarrow\Delta BMN=\Delta NPB\left(c.g.c\right)\)hay \(\Delta BMN\approx\Delta NPB\)
c) BM = 2 ; AB = 8 nên AM = 6
MNPB là hình bình hành nên NP = BM
Xét \(\Delta NPC\)và \(\Delta AMN\)có :
\(\widehat{PNC}=\widehat{MAN}\left(dv\right);\widehat{NPC}=\widehat{AMN}\left(=\widehat{ABC}\right)\)
\(\Rightarrow\)\(\Delta NPC\)\(\approx\)\(\Delta AMN\)( g.g )
\(\Rightarrow\)\(\frac{S_{NPC}}{S_{AMN}}=\left(\frac{NP}{AM}\right)^2=\left(\frac{BM}{AM}\right)^2=\left(\frac{2}{6}\right)^2=\frac{1}{9}\)

ta có AB=AM+MB=11+8=19 (cm)
xát tgAMN và tgABC có gA chung
gAMN = gABC (hai góc đồng vị của MN//BC)
=>tgAMN ~ tgABC (g.g)
=>AM/AB=AN/AC=>11/19=AN/38
=>AN=22 (cm)
ta có AC=AN+NC=>NC = 38-22=16(cm)

Ta có: AM+MB=AB(M nằm giữa A và B)
hay MB=AB-AM=12cm-8cm=4cm
Ta có: AN+NC=AC(N nằm giữa A và C)
hay AN+NC=18cm
Xét ΔABC có MN//BC(M∈AB; N∈AC)
nên \(\frac{AM}{MB}=\frac{AN}{NC}\)(định lí Ta lét)
\(\Leftrightarrow\frac{AM}{AN}=\frac{MB}{NC}\)
hay \(\frac{8}{AN}=\frac{4}{NC}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được
\(\frac{8}{AN}=\frac{4}{NC}=\frac{8+4}{AN+NC}=\frac{12}{18}=\frac{2}{3}\)
Do đó:
\(\left\{{}\begin{matrix}\frac{8}{AN}=\frac{2}{3}\\\frac{4}{NC}=\frac{2}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AN=\frac{8\cdot3}{2}=12cm\\NC=\frac{4\cdot3}{2}=6cm\end{matrix}\right.\)
Vậy: AN=12cm; NC=6cm