Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mình chỉ có thể cho cậu câu trả lời thôi
nếu mình chỉ cho câu trả lời thì cậu có **** mình không ?

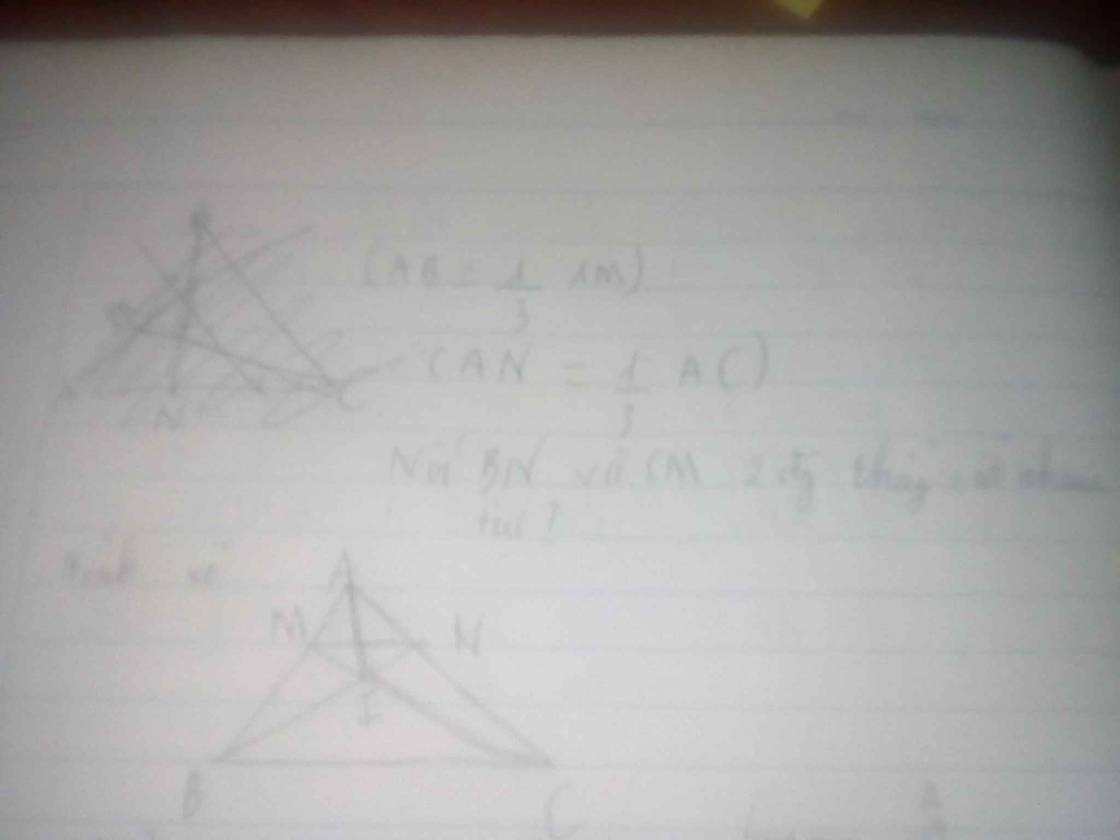 cái này là hình vẽ nhé!
cái này là hình vẽ nhé!
a, Tam giác AIB và tam giác ABC có chung chiều cao hạ từ B xuống AC, đáy AN = 1/3 đáy AC.
=> SAIB = 1/3 x S ABC.
Tam giác AIC và ABC có chiều cao hạ từ C xuống ABC, đáy AM = 1/3 đáy ABC.
=> SAIC = 1/3 x SABC.
=> SAIB = SAIC ( Vì cùng bằng = 1/3 SABC)
câu b thì bạn chưa nói rõ nên mình đưa bạn bản mẫu là tứ giác và 90cm2 nhé!
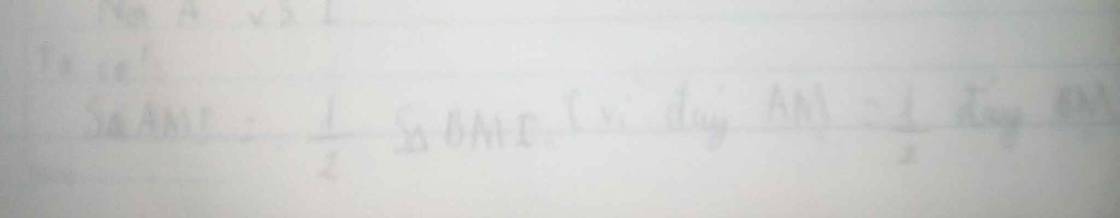 Ta có :
Ta có :
SAMI = 1/2 SƠMI ( vì đáy ÂM = 1/2 đáy BM)
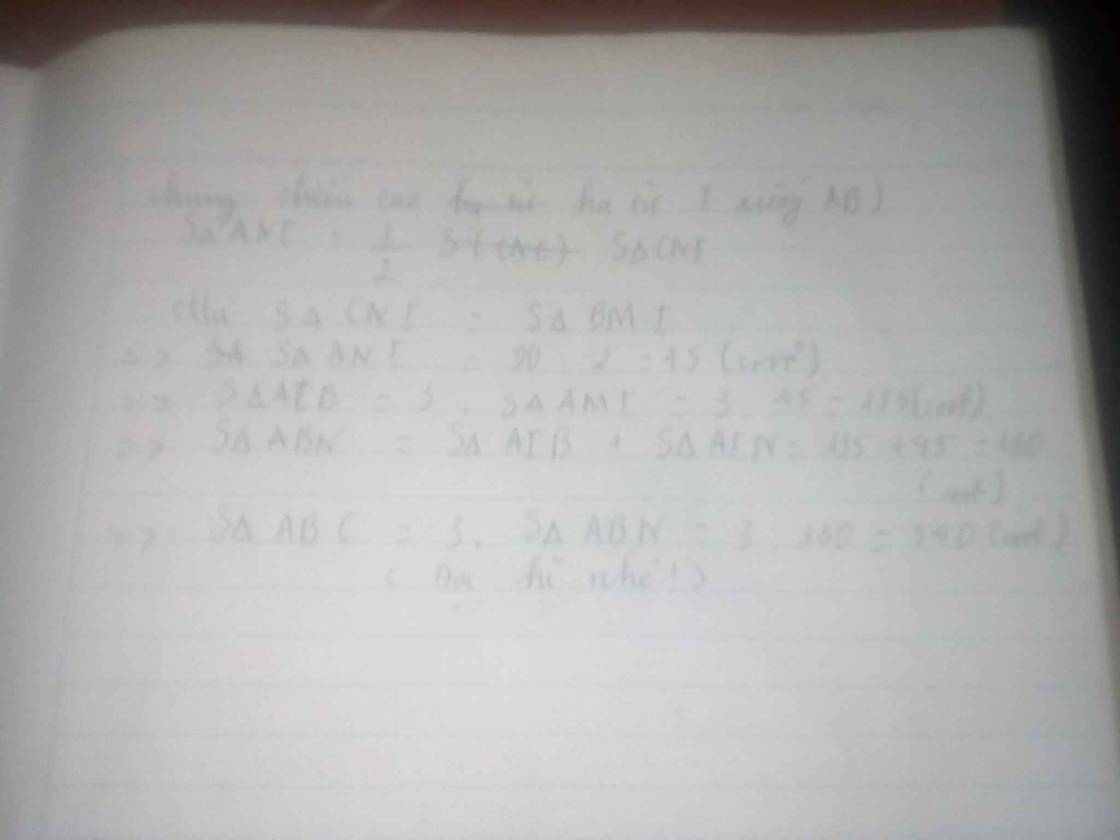 bạn thông cảm vì máy chụp hơi kém nhé!
bạn thông cảm vì máy chụp hơi kém nhé!

a) \(S_{ANB}=\dfrac{1}{2}\times S_{ABC}\) (chung đường cao hạ từ \(B\), \(AN=\dfrac{1}{2}\times AC\))
\(S_{AMC}=\dfrac{1}{2}\times S_{ABC}\) (chung đường cao hạ từ \(C\), \(AM=\dfrac{1}{2}\times AB\))
suy ra \(S_{AMC}=S_{ANB}\).
b) \(S_{MIB}=S_{ANB}-S_{AMIN},S_{NIC}=S_{AMC}-S_{AMIN}\)
mà \(S_{AMC}=S_{ANB}\) suy ra \(S_{MIB}=S_{NIC}\).
33
Diện tích tam giác ABC bằng \(205,5cm^2\) à bạn?
C A N M I B
a)
Xét tam giác CBM và tam giác ABC:
Chung chiều cùng từ C xuống AB
Đáy \(BM=\dfrac{2}{3}AB\)
\(\Rightarrow S_{BCM}=\dfrac{2}{3}S_{ABC}=137cm^2\)
b)
\(\dfrac{BM}{AB}=\dfrac{2}{3}\)
\(\dfrac{CN}{AC}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{BM}{AB}=\dfrac{CN}{AC}\)
MN song song AB
\(\Rightarrow\dfrac{MI}{CI}=\dfrac{NI}{BI}\)
\(\Rightarrow\dfrac{BI}{BN}=\dfrac{CI}{CM}\)
Xét tam giác BMI và tam giác BMN:
Chung chiều cao từ M xuống BN
Đáy BI và BN
\(\Rightarrow\dfrac{S_{BMI}}{S_{BMN}}=\dfrac{BI}{BN}\)
Tương tự, có:
\(\dfrac{S_{CIN}}{S_{CNM}}=\dfrac{CI}{CM}\)
Mà \(\dfrac{BI}{BN}=\dfrac{CI}{CM}\)
\(\Rightarrow\dfrac{S_{CIN}}{S_{CMN}}=\dfrac{S_{BMI}}{S_{BMN}}\)
Xét tam giác BMN và tam giác CMN:
Chung đáy MN
Chiều cao từ B xuống MN = chiều cao từ C xuống MN (BC song song MN)
\(\Rightarrow S_{BMN}=S_{CMN}\)
\(\Rightarrow S_{CIN}=S_{BIM}\).