Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ax, By là các tiếp tuyến của đường tròn (O)
=> Ax // By (cùng vuông góc với AB)
=> AMNB là hình thang
Hình thang AMNB có: OA = OB; IM = IN
=> OI là đường trung bình
=> OI // AM // BN
Lại có: AM, BN vuông góc với AB
=> IO vuông góc với AB
=> AB là tiếp tuyến của đường tròn (I;IO)

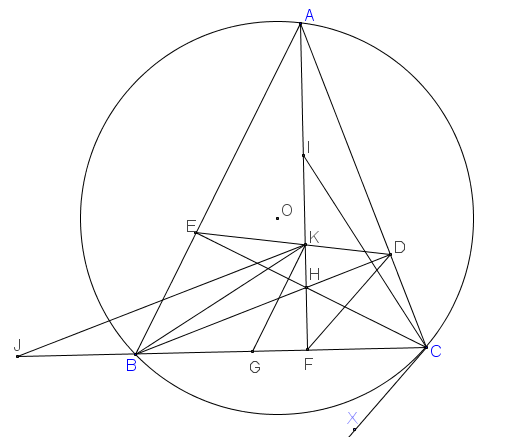
a . dễ c/m được tam giác AOF đồng dạng với ADB(gg)
b. Dễ c/m được tứ giác BHKD nt do DKB=DHB=90 cùng nhìn cạnh BD
nên DHK=KBD(cùng nhìn cạnh DK)
mà DCB=DBK(cùng phụ với KBC)
từ đó ta được DHK=DCO hay tứ giác KHOC nt
c, theo mk câu c sai đề vì nếu cần c.m \(\frac{BD}{DM}-\frac{DM}{AM}=1\Leftrightarrow DB\cdot AM=DM^2+DM\cdot AM=DM\left(AM+DM\right)=DM\cdot AD\)
(đến đây vẫn đúng nha bạn)
ta thấy AMC đồng dạng với ADB hay \(\frac{AM}{AD}=\frac{MC}{DB}\Rightarrow AM\cdot BD=CM\cdot AD\)\(\Rightarrow CM\cdot AD=DM\cdot AD\Leftrightarrow CM=DM\)(vô lý )
nên mk cho là đề sai nếu mk có sai bạn chỉ mk vs ạ

d)
Trên BF lấy điểm G sao cho GK //AB
=>KG⊥⊥CE (1) và BGBF=AKAFBGBF=AKAF (2)
theo câu c), DH là phân giác trong ˆKDFKDF^ (3)
=>HKHF=DKDFHKHF=DKDF (4)
có DA⊥⊥DH (5)
từ (3, 5) =>DA là phân giác ngoài ˆKDFKDF^
=>AKAF=DKDFAKAF=DKDF (6)
từ (2, 4, 6) =>BGBF=HKHFBGBF=HKHF (7)
trên tia đối tia BC lấy điểm J sao cho BJ =BG
=>BJBF=BGBFBJBF=BGBF (8)
từ (7, 8) =>BJBF=HKHFBJBF=HKHF
=>JK // BH
=>JK⊥⊥AC (8)
từ (1, 8) =>ˆJKG=ˆACHJKG^=ACH^ (9)
và có JF⊥⊥AH và (1)=>ˆKGJ=ˆCHAKGJ^=CHA^ (10)
từ (9, 10) =>△KGJ∼△CHA△KGJ∼△CHA (g, g)
=>KGCH=GJHA=2.GB2.HI=GBHIKGCH=GJHA=2.GB2.HI=GBHI (11)
từ (10, 11) =>△KGB∼△CHI△KGB∼△CHI (c, g, c)
=>ˆKBF=ˆCIFKBF^=CIF^
=>△FBK∼△FIC△FBK∼△FIC (đpcm)
và ˆICB+ˆFBKICB^+FBK^
=ˆBKF+ˆFBK=90∘=BKF^+FBK^=90∘
=>BK⊥CIBK⊥CI =>K là trực tâm của tam giác IBC (đpcm)
Hình gửi kèm
ủng hộ mình nha