Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

d) Tam giác ADB vuông tại D có: ∠(A1) + ∠(ABC) = 90o (1)
Tam giác BCF vuông tại F có: ∠(C1) + ∠(ABC) = 90o (2)
Từ (1)và (2) ⇒ ∠(A1) = ∠(C1)
Mặt khác, ta có: ∠( A 1 ) = ∠( C 2 ) ( 2 góc nội tiếp cùng chắn cung BM)
⇒ ∠( C 1 ) = ∠( C 2 )
⇒ CD là tia phân giác của góc HCM
Xét tam giác HCM có: CD vừa là tia phân giác vừa là đường cao (CD⊥HD)
⇒ Δ HCM cân tại C
⇒ CD cũng là trung tuyến của của HM hay H và M đối xứng với nhau qua D.

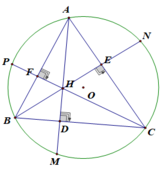
Đường tròn c: Đường tròn qua B_1 với tâm O Đoạn thẳng f: Đoạn thẳng [A, B] Đoạn thẳng g: Đoạn thẳng [A, C] Đoạn thẳng h: Đoạn thẳng [B, C] Đoạn thẳng l: Đoạn thẳng [P, C] Đoạn thẳng m: Đoạn thẳng [M, A] Đoạn thẳng n: Đoạn thẳng [B, N] O = (1.97, 2.92) O = (1.97, 2.92) O = (1.97, 2.92) Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm B: Điểm trên c Điểm B: Điểm trên c Điểm B: Điểm trên c Điểm C: Điểm trên c Điểm C: Điểm trên c Điểm C: Điểm trên c Điểm P: Giao điểm của c, j Điểm P: Giao điểm của c, j Điểm P: Giao điểm của c, j Điểm M: Giao điểm của c, k Điểm M: Giao điểm của c, k Điểm M: Giao điểm của c, k Điểm N: Giao điểm của c, i Điểm N: Giao điểm của c, i Điểm N: Giao điểm của c, i Điểm F: Giao điểm của j, f Điểm F: Giao điểm của j, f Điểm F: Giao điểm của j, f Điểm E: Giao điểm của i, g Điểm E: Giao điểm của i, g Điểm E: Giao điểm của i, g Điểm D: Giao điểm của k, h Điểm D: Giao điểm của k, h Điểm D: Giao điểm của k, h Điểm H: Giao điểm của l, m Điểm H: Giao điểm của l, m Điểm H: Giao điểm của l, m
a. Tứ giác CEHD có \(\widehat{HEC}=\widehat{HDC}=90^o\Rightarrow\) nó là tứ giác nội tiếp.
b. Tứ giác BFEC có \(\widehat{BEC}=\widehat{BFC}=90^o\Rightarrow\)nó là tứ giác nội tiếp. Vậy 4 điểm B, C, E, F cùng thuộc một đường tròn.
c. Ta thấy \(\Delta HAE\sim\Delta CAD\left(g-g\right)\Rightarrow\frac{AH}{AC}=\frac{AE}{AD}\Rightarrow AE.AC=AH.AD\)
Ta thấy \(\Delta CBE\sim\Delta CAD\left(g-g\right)\Rightarrow\frac{BC}{AC}=\frac{BE}{AD}\Rightarrow AD.BC=BE.AC\)
d. Ta thấy ngay \(\widehat{PCB}=\widehat{BAM}\) (Cùng phụ với góc ABC)
Mà \(\widehat{BAM}=\widehat{BCM}\) (Góc nội tiếp cùng chắn cung BM)
Vậy nên \(\widehat{PCB}=\widehat{BCM}\) hay CM là phân giác góc \(\widehat{PCB}\)
Lại có \(CM⊥HD\) nên HCM là tam giác cân. Vậy CB là trung trực của HM hay H, M đối xứng nhau qua BC.
e. Ta thấy BFHD là tứ giác nội tiếp nên \(\widehat{FDH}=\widehat{FBH}\) (Góc nội tiếp cùng chẵn cung FH)
DHEC cùng là tứ giác nội tiếp nên \(\widehat{HDE}=\widehat{HCE}\) (Góc nội tiếp cùng chẵn cung HE)
Mà \(\widehat{FBH}=\widehat{HCE}\) ( Cùng phụ với góc \(\widehat{BAC}\) )
nên \(\widehat{FDH}=\widehat{HDE}\) hay DH là phân giác góc FDE.
Tương tự FH, EH cũng là phân giác góc DFE và DEF.
Vậy tâm đường tròn nội tiếp tam giác DEF chính là H.

a:
H đối xứng K qua BC
=>BH=BK CH=CK
Xét ΔBHC và ΔBKC có
BH=BK
HC=KC
BC chung
=>ΔBHC=ΔBKC
=>góc BHC=góc BKC
góc BHC=180 độ-góc HBC-góc HCB
=90 độ-góc HBC+90 độ-góc HCB
=góc ABC+góc ACB
=180 độ-góc BAC
=>góc BAC+góc BHC=180 độ
=>góc BAC+góc BKC=180 độ
=>ABKC là tứ giác nội tiếp
b: Xét (O) có
ΔABM nội tiếp
AM là đường kính
=>ΔABM vuông tại B
=>BM//CH
Xét (O) có
ΔACM nội tiếp
AM là đường kinh
=>ΔACM vuông tại C
=>CM//BH
mà BM//CH
nên BHCM là hình bình hành
=>CB căt HM tại trung điểm của mỗi đường
=>H,I,M thẳng hàng

Trả lời:
P/s: Đề khó quá!~Chỉ làm đc 2 câu dễ!!! :D
a) Ta có ˆBEC=ˆBFC=900⇒BEC^=BFC^=900⇒ 2 điểm E, F cùng nhìn BC dưới 1 góc 900 nên 2 điểm E, F cùng thuộc đường tròn đường kính BC \(\Rightarrow\) BCEF là tứ giác nội tiếp đường tròn đường kính BC tâm M.
g) Ta có: ˆACB=ˆBAxACB^=BAx^(1) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AB).
Tứ giác BCEF là tứ giác nội tiếp (cmt) ⇒ˆACB+ˆEFB=1800⇒(Tổng 2 góc đối của tứ giác nội tiếp). Mà ˆEFB+ˆAFE=1800 (2 góc kề bù) ⇒ˆACB=ˆAFE=AFE^ (2).
Từ (1) và (2) ⇒ˆBAx=ˆAFE. Mà 2 góc này ở vị trí so le trong \(\Rightarrow\)Ax//EF
Mà OA⊥Ax (Do Ax là tiếp tuyến của đường tròn tại A).
Vậy OA⊥ EF.
~Học tốt!~