MA
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KB
0
21 tháng 9 2023
Tham khảo:
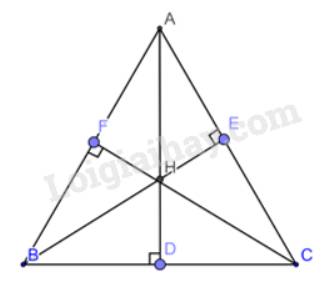
Xét tam giác BFC và tam giác BEC có :
BC chung
FC = BE
\(\widehat {BFC} = \widehat {BEC} = {90^o}\)
( cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat B\) ( 2 góc tương ứng ) (1)
Xét tam giác CFA và tam giác ADC ta có :
CF = AD
AC chung
\(\widehat {ADC} = \widehat {AFC} = {90^o}\)
(cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat A\)(2 góc tương ứng ) (2)
Từ (1) và (2) \( \Rightarrow \widehat C = \widehat A = \widehat B\) \( \Rightarrow \)Tam giác ABC là tam giác đều do có 3 góc bằng nhau
10 tháng 3 2017
a) Tự vẽ hình
xét tg BCF vuong tai f co bm=mc(gt) => mf la trg tuyên thuoc cạnh huyen nên mf= mc=mb hay mf=1/2 bc (1)
tuong tu tg bec vuog tai e có me = 1/2 bc(2)
tu (1) va (2) có me= mf => tg mef cân
b) tứ giác FECB nội tiếp trong đuong tròn có tam là M và đuong kính là BC nên 2 góc đối fec + fbc =180o
c) góc feb = fcb ( cùng chắn cung bf)
c)
NH
Cho tam giác ABC nhọn. Kẻ các đường vuông góc AH,BE,CF.
Chứng minh rằng: AH+BE+CF<Chu vi tam giác ABC
0
NH
1
27 tháng 2 2023
Xét ΔAFC vuông tại F và ΔAEB vuông tại E có
CF=BE
góc ACF=gócABE
=>ΔAFC=ΔAEB
=>AC=AB
Xét ΔCEB vuông tại E và ΔCDA vuông tại D có
EB=DA
góc C chung
=>ΔCEB=ΔCDA
=>CB=CA=AB
=>ΔABC đều