Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho tam giác ABC nhọn. Kẻ các đường vuông góc AH,BE,CF.
Chứng minh rằng: AH+BE+CF<Chu vi tam giác ABC


Tham khảo:
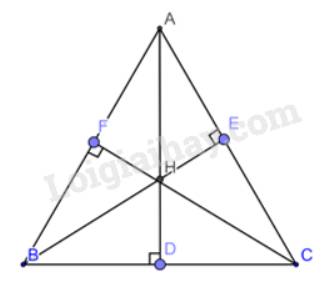
Xét tam giác BFC và tam giác BEC có :
BC chung
FC = BE
\(\widehat {BFC} = \widehat {BEC} = {90^o}\)
( cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat B\) ( 2 góc tương ứng ) (1)
Xét tam giác CFA và tam giác ADC ta có :
CF = AD
AC chung
\(\widehat {ADC} = \widehat {AFC} = {90^o}\)
(cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat A\)(2 góc tương ứng ) (2)
Từ (1) và (2) \( \Rightarrow \widehat C = \widehat A = \widehat B\) \( \Rightarrow \)Tam giác ABC là tam giác đều do có 3 góc bằng nhau

a) Vì MD là trung trực AB trong ∆AMD
=> ∆AMD cân tại A
=> AM = AD
Vì DN là trung trực AC trong ∆ADN
=>∆ADN cân tại A
=> AD = AN
Mà AM = AD
=> AM = AN
=> ∆AMN cân tại A

a: góc AFH+góc AEH=180 độ
góc AFH=góc AEH=90 độ
=>AEHF nội tiếp đường tròn đường kính AH
=>NF=NE
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp đường tròn đường kính BC
=>MF=ME
=>NM là trung trực của EF
b: góc MEN=góc MEH+góc NEH
=góc MBE+góc NHE
=góc MBE+90 độ-góc MBE=90 độ
=>góc MFN=90 độ

sorry mk ko bít làm dù đag hok lớp 7!!!!!!!
5645756