Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Xét tứ giác AFDC. Có
góc BFC= góc BEC=90( Giả thiết)
mà BFC và BEC là hai goc kề một cạnh và cùng nhìn cạnh AC
=> Tứ giác AFDC nội tiếp( quĩ tích cung chứa góc)

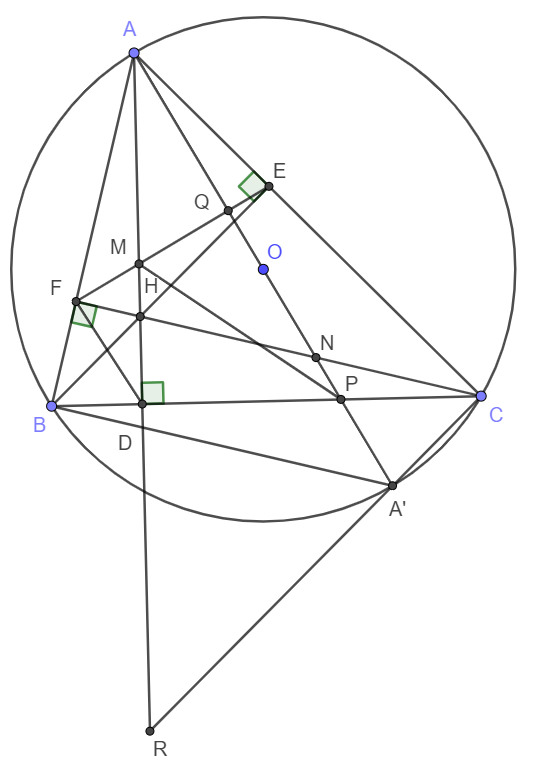
a) theo gt, BFC=BEC=90
=> BFEC nội tiếp (có 2 góc kề bang nhau)
góc AFC=ADC=90 => AFDC nội tiếp ( có 2 cạnh kề cùng nhìn một đoan thẳng bằng nhau)
b) vì tứ giác ABA'C nội tiếp => ABC = AA'C (cùng chắn cung AC)
Lại có ABC= AHF (Cùng phụ với góc BAD)
Ta thấy AFHE nội tiếp vì AFH +AEH = 90+90=180
=> AHF=AEF (Cùng chắn cung AF)
=>Đpcm
c) vì tứ giác EQA'C nôi tiếp
nên EQA'+ECA'=180 mà ECA'=90 vì là góc nội tiếp chắn nửa đường tròn
=> MQP=EQA'=90 ( vì MQP+EQA=180)
Trong đó ADC=90 =>Đpcm
d) Vì ABA'C VÀ FBDH nội tiếp nên góc NA'C=ABC=DHC
=>NA'C=DHC=>Đpcm

ta có
\(\widehat{AEH}=90^0;\widehat{AFH}=90^0\)
=> \(\widehat{AEH}+\widehat{AFH}=180^0\)
=> tứ giác AEHF nội tiếp được nhé
ta lại có AEB=ADB=90 độ
=> E , D cùng nhìn cạnh AB dưới 1 góc zuông
=> tứ giác AEDB nội tiếp được nha
b)ta có góc ACK = 90 độ ( góc nội tiếp chắn nửa đường tròn)
hai tam giác zuông ADB zà ACK có
ABD = AKC ( góc nội tiếp chắn cung AC )
=> tam giác ABD ~ tam giác AKC (g.g)
c) zẽ tiếp tuyến xy tại C của (O)
ta có OC \(\perp\) Cx (1)
=> góc ABC = góc DEC
mà góc ABC = góc ACx
nên góc ACx= góc DEC
do đó Cx//DE ( 2)
từ 1 zà 2 suy ra \(OC\perp DE\)
a: Xét tứ giác AFDC có
\(\widehat{AFC}=\widehat{ADC}=90^0\)
Do đó: AFDC là tứ giác nội tiếp
b: \(\widehat{EFC}=\widehat{EAH}=\widehat{CAD}\)
\(\widehat{DFC}=\widehat{EBC}\)
mà \(\widehat{CAD}=\widehat{EBC}\)
nên \(\widehat{EFC}=\widehat{DFC}\)
hay FH là tia phân giác của góc EFD(1)
\(\widehat{FEH}=\widehat{BAD}\)
\(\widehat{DEH}=\widehat{FCB}\)
mà \(\widehat{BAD}=\widehat{FCB}\)
nên \(\widehat{FEH}=\widehat{DEH}\)
hay EH là tia phân giác của góc FED(2)
Từ (1) và (2) suy ra H là giao của các đường phân giác của ΔDEF