Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(1,\)Gọi I là tâm đường tròn đường kính BC thì I là trung điểm BC và \(MI=IN=BI=CI=\dfrac{1}{2}BC\) (bán kính cùng đường tròn)
\(\Rightarrow\Delta BNC\) vuông tại N và \(\Delta CMB\) vuông tại N
Vậy \(\widehat{BMC}=\widehat{BNC}=90\) độ
\(2,\)Ta có \(H=BM\cap CN\)
Mà BM, CN là đường cao tam giác ABC
Suy ra H là trực tâm
\(\Rightarrow AH\) là đường cao thứ 3
\(\Rightarrow AH\perp BC\)
\(3,\) Gọi giao điểm của tiếp tuyến tại N và AH là K, AH cắt BC tại E.
Ta có \(\widehat{KNH}+\widehat{INH}=90\)
Mà \(\widehat{INH}=\widehat{NCI}\left(NI=IC\right)\)
\(\Rightarrow\widehat{KNH}+\widehat{NCI}=90\)
Mà \(\widehat{NCI}+\widehat{CHE}=90\)
\(\Rightarrow\widehat{KNH}=\widehat{CHE}\)
Mà \(\widehat{CHE}=\widehat{NHK}\left(đđ\right)\)
\(\Rightarrow\widehat{KNH}=\widehat{NHK}\)
\(\Rightarrow\Delta NHK\) cân tại K\(\Rightarrow NK=KH\left(1\right)\)
Ta có \(\widehat{KNH}+\widehat{KNA}=90;\widehat{KHN}+\widehat{NAH}=90\)
\(\Rightarrow\widehat{ANK}=\widehat{NAK}\Rightarrow NK=AK\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow NK=KH=AK\)
\(\Rightarrow\)Đfcm
Tick plzzz, nghĩ nát óc đó
1: Xét (O) có
\(\widehat{BNC}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{BNC}=90^0\)
Xét (O) có
\(\widehat{BMC}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{BMC}=90^0\)
2: Xét ΔABC có
BM là đường cao ứng với cạnh AC
CN là đường cao ứng với cạnh AB
BM cắt CN tại H
Do đó: H là trực tâm của ΔABC
Suy ra: AH\(\perp\)BC

Lời giải:
a. Ta có:
$\widehat{BNC}=\widehat{BMC}=90^0$ (góc nt chắn nửa đường tròn - cung BC)
$\Rightarrow BN\perp AC, CM\perp AB$
Tam giác $ABC$ có 2 đường cao $BN, CM$ cắt nhau tại $H$ nên $H$ là trực tâm của tam giác $ABC$.
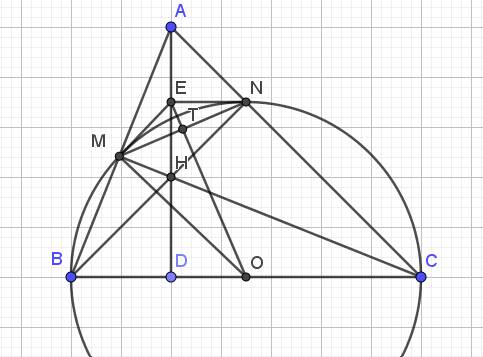
b. Gọi $D$ là giao của $AH$ và $BC$. Do $H$ là trực tâm tam giác $ABC$ nên $AH\perp BC$ tại $D$.
Tam giác $BMC$ vuông tại $M$
$\Rightarrow$ trung tuyến $MO= \frac{BC}{2}=BO$ (đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền)
$\Rightarrow BOM$ là tam giác cân tại $O$
$\Rightarrow \widehat{OMB}=\widehat{OBM}=90^0-\widehat{BCM}$
$=90^0-\widehat{DCH}=\widehat{MHA}=\widehat{MHE}(1)$
$CM\perp AB$ nên $AMH$ là tam giác vuông tại $M$
$\Rightarrow ME=\frac{AH}{2}=EH$ (đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền)
$\Rightarrow MEH$ cân tại $E$
$\Rightarrow \widehat{MHE}=\widehat{EMH}(2)$
Từ $(1); (2)\Rightarrow \widehat{OMB}=\widehat{EMH}$
$\Rightarrow \widehat{OMB}+\widehat{OMC}=\widehat{EMH}+\widehat{OMC}$
$\Rightarrow \widehat{BMC}=\widehat{EMO}$
$\Rightarrow \widehat{EMO}=90^0$
$\Rightarrow EM\perp MO$ nên $EM$ là tiếp tuyến $(O)$
c.
Ta có:
$EM=\frac{AH}{2}=EN$
$OM=ON$
$\Rightarrow EO$ là trung trực của $MN$
Gọi $T$ là giao điểm $EO, MN$ thì $EO\perp MN$ tại $T$ và $T$ là trung điểm $MN$.
Xét tam giác $EMO$ vuông tại $M$ có $MT\perp EO$ thì:
$ME.MO = MT.EO = \frac{MN}{2}.EO$
$\Rightarrow 2ME.MO = MN.EO$

a: Xét (O) có
ΔBMC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBMC vuông tại M
Xét (O) có
ΔBNC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBNC vuông tại N
Xét ΔBAC có
BN là đường cao ứng với cạnh huyền AC
CM là đường cao ứng với cạnh huyền AB
BN cắt CM tại H
Do đó: AH⊥BC