Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ân tích và giải quyết: Tam giác ABC và đường tròn nội tiếp: Tam giác ABC là tam giác nhọn và có ba góc nhọn, tức là tất cả các góc trong tam giác đều nhỏ hơn 90°. Tam giác ABC nội tiếp một đường tròn với tâm O (đường tròn này gọi là đường tròn ngoại tiếp của tam giác ABC). Do đó, các điểm A, B, C nằm trên đường tròn này. Đường cao AD và CE: Đường cao AD từ đỉnh A vuông góc với BC, và đường cao CE từ đỉnh C vuông góc với AB. Các đường cao này có những tính chất đặc biệt như chúng đồng quy tại trực tâm của tam giác ABC. Tiếp tuyến tại A của (O) cắt BC tại M: Tiếp tuyến tại điểm A của đường tròn (O) cắt cạnh BC tại điểm M. Tính chất của tiếp tuyến cho ta rằng đoạn AM vuông góc với bán kính OA của đường tròn tại A. Tiếp tuyến thứ hai tại M cắt (O) tại N: Từ điểm M, ta kẻ tiếp tuyến thứ hai đến đường tròn (O), tiếp tuyến này cắt đường tròn tại N. Do tính chất của tiếp tuyến, ta có các đặc điểm quan trọng như AM = AN (do tính chất của tiếp tuyến với đường tròn). Vẽ CK vuông góc với AN tại K: Kẻ đoạn CK vuông góc với AN tại điểm K. Do CK vuông góc với AN, ta có những quan hệ đặc biệt giữa các điểm này. Chứng minh DK đi qua trung điểm của đoạn thẳng BE: Để chứng minh DK đi qua trung điểm của đoạn BE, ta cần sử dụng các tính chất của hình học phẳng, đặc biệt là các định lý liên quan đến đường cao, tiếp tuyến và trung điểm của đoạn thẳng. Cần chứng minh rằng DK chia đoạn BE thành hai đoạn bằng nhau, tức là DK đi qua trung điểm của BE. Điều này có thể được thực hiện bằng cách sử dụng các tính chất đối xứng của tam giác và các định lý về tiếp tuyến. Kết luận: Bằng cách sử dụng các tính chất hình học của tam giác, các đường cao, các tiếp tuyến và đối xứng trong tam giác nội tiếp, ta có thể chứng minh rằng DK đi qua trung điểm của đoạn BE. Đây là một bài toán phức tạp yêu cầu sự am hiểu về các định lý hình học cơ bản và nâng cao.

A B C O D E K M F T y x
c) Gọi T là giao điểm thứ hai của FD với đường tròn (O). Ta c/m EO đi qua T.
Ta có: ^ADM = ^DAC + ^DCA = ^BAC/2 + ^ACB = ^BAD + ^MAB = ^MAD => \(\Delta\)DAM cân tại M => MA=MD
Lại có: MA và MF là 2 tiếp tuyến của (O) nên MA=MF. Do đó: MD=MF => \(\Delta\)MDF cân tại M (đpcm).
Dễ thấy: \(\Delta\)MAB ~ \(\Delta\)MCA (g.g) và \(\Delta\)MFB ~ \(\Delta\)MCF (g.g)
=> \(\frac{MA}{MC}=\frac{MF}{MC}=\frac{AB}{AC}=\frac{BD}{CD}=\frac{FB}{FC}\) => FD là tia phân giác ^BFC (1)
Kẻ tia đối Fy của FB => ^EFy = ^ECB = ^EBC = ^EFC => FE là phân giác ^CFy (2)
Từ (1) và (2) suy ra: FD vuông góc với FE (Vì ^BFC + ^CFy = 1800) hay ^EFT = 900
=> ET là đường kính của (O) => ET trùng với OE => OE đi qua T => ĐPCM.
d) Áp dụng ĐL Ptolemy có tứ giác BFCT nội tiếp có: BF.CT + CF.BT = BC.FT
=> CT.(BF+CF) = BC.FT => \(BF+CF=\frac{BC.FT}{CT}\le\frac{BC.ET}{CT}=\frac{2CK.ET}{CT}=2EC=2BE\)
Dấu "=" xảy ra khi F trùng với E <=> MF vuông góc OE <=> MF // BC => M không nằm trên BC (mâu thuẫn)
=> Không có dấu "=" => BF+CF < 2BE (đpcm).

Cho tam giác ABCABC không có góc tù (AB < AC)(AB<AC), nội tiếp đường tròn (O; R)(O;R), (BB, CC cố định, AA di động trên cung lớn BC). Các tiếp tuyến tại BB và CC cắt nhau tại MM. Từ MM kẻ đường thẳng song song với ABAB, đường thẳng này cắt (O)(O) tại DD và EE (DD thuộc cung nhỏ BCBC), cắt BCBC tại FF, cắt ACAC tại II. Chứng minh rằng \widehat{MBC}=\widehat{BAC}MBC=BAC . Từ đó suy ra MBICMBIC là tứ giác nội tiếp.
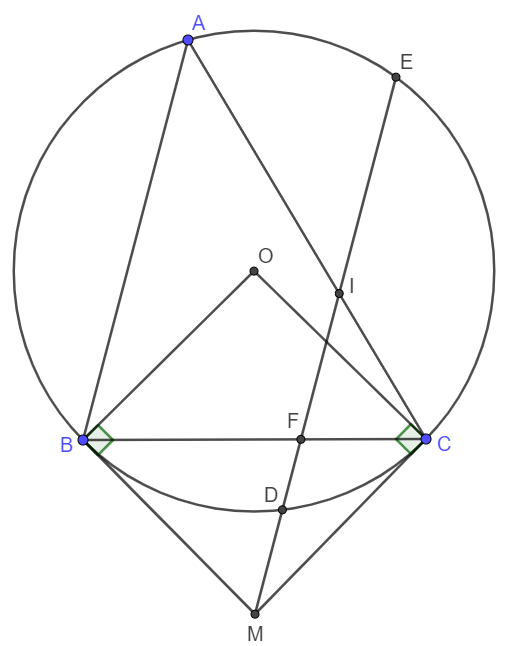
theo gt, ta co:
goc MBC= BAC (cung chan cung BC)
mat khac, ta lai co goc BAC = MIC ( dong vi)
=> goc MBC= MIC
=> tu giac BICM noi tiep
khó quá bạn ơi