Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

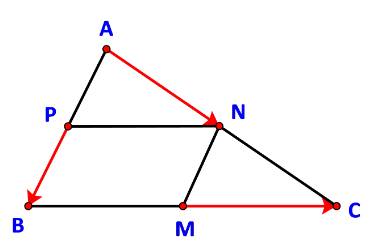
Do M, N, P lần lượt là trung điểm của BC, CA, AB
\( \Rightarrow MN = \frac{{AB}}{2} = PB\) và MN // PB.
\( \Rightarrow \overrightarrow {PB} = \overrightarrow {NM} \)
Ta có: \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {NM} + \overrightarrow {MC} = \overrightarrow {NC} \)
Lại có: \(\overrightarrow {NC} = \overrightarrow {AN} \) (do N là trung điểm của AC)
Vậy \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {AN} \)

\(\overrightarrow{AN}=\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}=\frac{\overrightarrow{AB}}{2}+\frac{\overrightarrow{AC}}{2}=\overrightarrow{AM}+\overrightarrow{AP}\)
\(\overrightarrow{AN}=\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}\)
\(\overrightarrow{BP}=\frac{\overrightarrow{BA}+\overrightarrow{BC}}{2}\)
\(\overrightarrow{CM}=\frac{\overrightarrow{CB}+\overrightarrow{CA}}{2}\)
\(\Rightarrow\overrightarrow{AN}+\overrightarrow{BP}+\overrightarrow{CM}=\frac{\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{CA}+\overrightarrow{BC}+\overrightarrow{CB}}{2}=\overrightarrow{0}\)

A B C M N P
\(\left\{{}\begin{matrix}\overrightarrow{MN}=\overrightarrow{PC}\\\overrightarrow{MP}=\overrightarrow{NC}\\\overrightarrow{PN}=\overrightarrow{MB}\end{matrix}\right.\)
Bạn xem lại nha, có thể đáp án A hoặc B sẽ có \(\overrightarrow{MN}=\overrightarrow{PC}\)

a) Vì M, N, P lần lượt là trung điểm của BC, CA, AB
Nên AM, BN, CP lần lượt là đường trung tuyến của BC, CA, AB.
\(\Rightarrow\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}=\overrightarrow{0}\)
Lời giải:
a)
\(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}=\overrightarrow{AB}+\overrightarrow{BM}+\overrightarrow{BC}+\overrightarrow{CN}+\overrightarrow{CA}+\overrightarrow{AP}\)
\(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}=\overrightarrow{AC}+\overrightarrow{CM}+\overrightarrow{BA}+\overrightarrow{AN}+\overrightarrow{CB}+\overrightarrow{BP}\)
\(\Rightarrow 2(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP})=(\overrightarrow{AB}+\overrightarrow{BA})+(\overrightarrow{BM}+\overrightarrow{CM})+(\overrightarrow{BC}+\overrightarrow{CB})+(\overrightarrow{CA}+\overrightarrow{AC})+(\overrightarrow{AP}+\overrightarrow{BP})+(\overrightarrow{CN}+\overrightarrow{AN})\)
\(=\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0}\) (do các cặp tổng đều là vecto đối nhau)
\(\Rightarrow \overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}=0\)
(đpcm)
b) Theo phần a:
\(\overrightarrow{AM}=-(\overrightarrow{BN}+\overrightarrow{CP})=-\overrightarrow{BN}+(-\overrightarrow{CP})\)
\(=\overrightarrow{NB}+\overrightarrow{PC}\) (đpcm)

a/
\(\overrightarrow{AN}+\overrightarrow{CM}-\overrightarrow{PB}=\frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{CB}-\frac{1}{2}\overrightarrow{AB}\)
\(=\frac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{CB}\right)+\frac{1}{2}\overrightarrow{BA}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BA}=\overrightarrow{0}\)
b/
\(\overrightarrow{AP}+\overrightarrow{BM}+\overrightarrow{MP}=\overrightarrow{AP}+\overrightarrow{BP}=\overrightarrow{0}\)

a) Chữa đề: \(\overrightarrow{CA}+\overrightarrow{DB}=\overrightarrow{CB}+\overrightarrow{DA}=2\overrightarrow{NM}\)
\(Ta\text{ }có:\overrightarrow{CA}+\overrightarrow{DB}=\overrightarrow{CB}+\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AB}\\ =\overrightarrow{CB}+\overrightarrow{DA}+\left(\overrightarrow{BA}+\overrightarrow{AB}\right)=\overrightarrow{CB}+\overrightarrow{DA}\)
\(\)\(\overrightarrow{CA}+\overrightarrow{DB}=\overrightarrow{CA}+\overrightarrow{CB}+\overrightarrow{DC}\\ =2\overrightarrow{CM}+2\overrightarrow{NC}=2\left(\overrightarrow{NC}+\overrightarrow{CM}\right)=2\overrightarrow{NM}\)
Vậy \(\overrightarrow{CA}+\overrightarrow{DB}=\overrightarrow{CB}+\overrightarrow{DA}=2\overrightarrow{NM}\)
\(\text{b) }\overrightarrow{AD}+\overrightarrow{BD}+\overrightarrow{AC}+\overrightarrow{BC}=-\left(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{CA}+\overrightarrow{CB}\right)\\ =-\left[\left(\overrightarrow{DA}+\overrightarrow{DB}\right)+\left(\overrightarrow{CA}+\overrightarrow{CB}\right)\right]\\ =-\left(2\overrightarrow{DM}+2\overrightarrow{CM}\right)=2\left(\overrightarrow{MD}+\overrightarrow{MC}\right)=4\left(\overrightarrow{MN}\right)\)
\(\text{c) }2\left(\overrightarrow{AB}+\overrightarrow{AI}+\overrightarrow{NA}+\overrightarrow{DA}\right)\\ =2\left[\left(\overrightarrow{AB}+\overrightarrow{DA}\right)+\left(\overrightarrow{AI}+\overrightarrow{NA}\right)\right]\\ =2\left[\left(\overrightarrow{AB}+\overrightarrow{BA}+\overrightarrow{DB}\right)+\overrightarrow{NI}\right]=2\left(\overrightarrow{DB}+\overrightarrow{NI}\right)\)
Mà IN là dường trung bình \(\Delta BCD\)
\(\Rightarrow\left\{{}\begin{matrix}IN//BD\\IN=\frac{1}{2}BD\end{matrix}\right.\Rightarrow\overrightarrow{IN}=\frac{1}{2}\overrightarrow{BD}\\ \Rightarrow2\left(\overrightarrow{AB}+\overrightarrow{AI}+\overrightarrow{NA}+\overrightarrow{DA}\right)\\ =2\left(\overrightarrow{DB}+\overrightarrow{NI}\right)=2\left(\overrightarrow{DB}+\frac{1}{2}\overrightarrow{DB}\right)=2\cdot\frac{3}{2}\overrightarrow{DB}=3\overrightarrow{DB}\)
a) Ta có: \(\overrightarrow {BC} ,\overrightarrow {PN} \) là hai vecto cùng hướng và \(\frac{1}{2}\left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {PN} } \right|\)
\( \Rightarrow \frac{1}{2}\overrightarrow {BC} = \overrightarrow {PN} \)\( \Rightarrow \overrightarrow {AP} + \frac{1}{2}\overrightarrow {BC} = \overrightarrow {AP} + \overrightarrow {PN} = \overrightarrow {AN} \)
b) Ta có: \(\overrightarrow {MP} ,\overrightarrow {CA} \) là hai vecto cùng hướng và \(2\left| {\overrightarrow {MP} } \right| = \left| {\overrightarrow {CA} } \right|\)
\( \Rightarrow 2\overrightarrow {MP} = \overrightarrow {CA} \)\( \Rightarrow \overrightarrow {BC} + 2\overrightarrow {MP} = \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow {BA} \)