Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
\(AB > AC \Rightarrow \widehat {ABC} < \widehat {ACB}\)( quan hệ giữa góc và cạnh đối diện trong tam giác ABC)
\(\begin{array}{l} \Rightarrow {180^0} - \widehat {ABD} < {180^0} - \widehat {ACE}\\ \Rightarrow \widehat {ABD} > \widehat {ACE}\end{array}\)
Vì BD= BA nên tam giác ABD cân tại B \( \Rightarrow \widehat {ABD} = {180^0} - 2\widehat {ADB}\)
Vì CE = CA nên tam giác ACE cân tại C \( \Rightarrow \widehat {ACE} = {180^0} - 2\widehat {AEC}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {{180}^0} - 2\widehat {ADB} > {{180}^0} - 2\widehat {AEC}}\\{ \Rightarrow \widehat {ADB} < \widehat {AEC}}\\{Hay{\mkern 1mu} \widehat {ADE} < \widehat {AED}}\end{array}\)
b) Xét tam giác ADE ta có : \(\widehat {ADB} < \widehat {AEC}\)
\( \Rightarrow AD > AE\)(Quan hệ giữa cạnh và góc đối diện trong tam giác).

Giải thích các bước giải:
Trong có góc BAD tù nên góc BAD > góc ADB => BD > BA. (1)
Ta có góc BDE = góc BAD + góc ABD (vì …)
Suy ra góc BDE là góc tù, vậy góc BDE là góc lớn nhất trong 3 góc của tam giác BDE.
Trong tam giác BDE ta có: góc BDE > gocsBED => BE > BD. (2)
Tương tự có góc BEC tù, trong tam giác BEC có góc BEC > góc BCE => BC > BE (3)
Từ 1, 2 và 3 suy ra: BA < BD < BE < BC

A B C D E
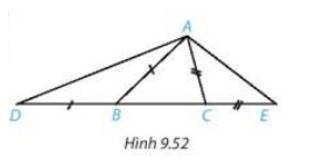
Xét \(\Delta ABD\)có \(\widehat{A}\)tù \(\Rightarrow BA< BD\)(1); \(\widehat{ADB}< 90^o\)
\(\Rightarrow\widehat{BDE}>90^o\)\(\Rightarrow\Delta BDE\)tù tại D \(\Rightarrow BD< BE\)(2); \(\widehat{BED}< 90^o\)
\(\Rightarrow\widehat{BEC}>90^o\)\(\Rightarrow\Delta BEC\)tù tại E \(\Rightarrow BE< BC\)(3)
Từ (1), (2), (3) \(\Rightarrow BA< BD< BE< BC\left(đpcm\right)\)
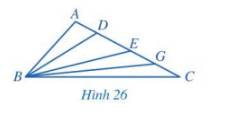
Xét tam giác BAD:
+ Góc A tù (góc > 90°) nên cạnh BD là cạnh lớn nhất trong tam giác này (đối diện với góc A).
Nên BD > BA.
+ Góc A tù nên góc ABD và góc ADB là góc nhọn → góc BDE là góc tù (ba điểm A, D, E thẳng hàng hay góc ADE =180°). Vậy BE (đối diện với góc BDE) > BD.
Tương tự, ta có:
+ Góc BDE là góc tù nên góc DBE và góc DEB là góc nhọn → góc BEG là góc tù. Vậy BG > BE.
+ Góc BEG là góc tù nên góc EBG và góc EGB là góc nhọn → góc BGC là góc tù. Vậy BC > BG.
Vậy BA < BD <BE < BG < BC.
Hay các đoạn thẳng BA, BD, BE, BG, BC theo thứ tự tăng dần là: BA, BD, BE, BG, BC.