Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

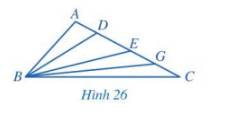
Xét tam giác BAD:
+ Góc A tù (góc > 90°) nên cạnh BD là cạnh lớn nhất trong tam giác này (đối diện với góc A).
Nên BD > BA.
+ Góc A tù nên góc ABD và góc ADB là góc nhọn → góc BDE là góc tù (ba điểm A, D, E thẳng hàng hay góc ADE =180°). Vậy BE (đối diện với góc BDE) > BD.
Tương tự, ta có:
+ Góc BDE là góc tù nên góc DBE và góc DEB là góc nhọn → góc BEG là góc tù. Vậy BG > BE.
+ Góc BEG là góc tù nên góc EBG và góc EGB là góc nhọn → góc BGC là góc tù. Vậy BC > BG.
Vậy BA < BD <BE < BG < BC.
Hay các đoạn thẳng BA, BD, BE, BG, BC theo thứ tự tăng dần là: BA, BD, BE, BG, BC.

Giải thích các bước giải:
Trong có góc BAD tù nên góc BAD > góc ADB => BD > BA. (1)
Ta có góc BDE = góc BAD + góc ABD (vì …)
Suy ra góc BDE là góc tù, vậy góc BDE là góc lớn nhất trong 3 góc của tam giác BDE.
Trong tam giác BDE ta có: góc BDE > gocsBED => BE > BD. (2)
Tương tự có góc BEC tù, trong tam giác BEC có góc BEC > góc BCE => BC > BE (3)
Từ 1, 2 và 3 suy ra: BA < BD < BE < BC

A B C D E
Xét \(\Delta ABD\)có \(\widehat{A}\)tù \(\Rightarrow BA< BD\)(1); \(\widehat{ADB}< 90^o\)
\(\Rightarrow\widehat{BDE}>90^o\)\(\Rightarrow\Delta BDE\)tù tại D \(\Rightarrow BD< BE\)(2); \(\widehat{BED}< 90^o\)
\(\Rightarrow\widehat{BEC}>90^o\)\(\Rightarrow\Delta BEC\)tù tại E \(\Rightarrow BE< BC\)(3)
Từ (1), (2), (3) \(\Rightarrow BA< BD< BE< BC\left(đpcm\right)\)

Giải thích các bước giải:
a)Xét tam giác BAD và tam giác BED:
BD:cạnh chung
^ABD=^EBD (vì BD là tia phân giác của ^ABC)
AB=BE(gt)
=>tam giác BAD=tam giác BED(c.g.c)
b)Từ tam giác BAD=tam giác BED(cmt)
=>AD=DE(cặp cạnh t.ứ)
và ^BAD=^BED(cặp góc .tứ),mà ^BAD=900 (^BAC=900)=>^BED=900
Xét tam giác DFA vuông ở A và tam giác DCE vuông ở E có:
AD=AE (cmt)
^ADF=^EDC (2 góc đối đỉnh)
=>tam giác DFA=tam giác DCE(cgv-gnk)
=>DF=DC(cặp cạnh t.ứ)
=>tam giác DFC cân tại D (dấu hiệu nhận biết tam giác cân)
c)Từ tam giác DFA=tam giác DCE (cmt)
=>AF=CE(cặp cạnh t.ứ)
Ta có: BE+CE=BC
BA+AF=BF
mà AF=CE(cmt),AB=AE(gt)
=>BC=BF
=>tam giác BFC cân tại B (dấu hiệu nhận biết tam giác cân)
=>^BCF=1800−FBC21800−FBC2 (tính chất tam giác cân) (1)
Vì AB=AE(gt)
=>tam giác ABE cân tại B (dấu hiệu nhận biết tam giác cân)
=>^BEA=1800−ABE21800−ABE2 (tính chất tam giác cân) (2)
Từ (1);(2);lại có ^ABE=^FBC
=>^BCF=^BEA,mà 2 góc này nằm ở vị trí đồng vị
=>AE//CF(dấu hiệu nhận biết 2 đg thẳng song song)

góc CAD>90 độ
=>góc CED>90 độ
=>ED<CD
goc CDB=góc DAC+góc ACD
=>góc CDB>90 độ
=>CD<BC
=>ED<BC