Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em tham khảo bài dưới đây:
Câu hỏi của ngô thị gia linh - Toán lớp 8 - Học toán với OnlineMath
a) \(\Delta AME=\Delta AHE\) (Hai cạnh góc vuông)

Đoạn thẳng f: Đoạn thẳng [A, B] Đoạn thẳng g: Đoạn thẳng [B, C] Đoạn thẳng h: Đoạn thẳng [A, C] Đoạn thẳng j: Đoạn thẳng [A, H] Đoạn thẳng k: Đoạn thẳng [H, M] Đoạn thẳng l: Đoạn thẳng [N, H] Đoạn thẳng m: Đoạn thẳng [M, N] Đoạn thẳng n: Đoạn thẳng [A, N] Đoạn thẳng p: Đoạn thẳng [A, M] Đoạn thẳng q: Đoạn thẳng [E, F] Đoạn thẳng r: Đoạn thẳng [A, I] Đoạn thẳng t: Đoạn thẳng [I, D] A = (9.91, 10.29) A = (9.91, 10.29) A = (9.91, 10.29) B = (3.97, -8.27) B = (3.97, -8.27) B = (3.97, -8.27) C = (33.4, -8.47) C = (33.4, -8.47) C = (33.4, -8.47) Điểm H: Giao điểm đường của i, g Điểm H: Giao điểm đường của i, g Điểm H: Giao điểm đường của i, g Điểm M: H đối xứng qua f Điểm M: H đối xứng qua f Điểm M: H đối xứng qua f Điểm N: H đối xứng qua h Điểm N: H đối xứng qua h Điểm N: H đối xứng qua h Điểm E: Giao điểm đường của f, k Điểm E: Giao điểm đường của f, k Điểm E: Giao điểm đường của f, k Điểm F: Giao điểm đường của h, l Điểm F: Giao điểm đường của h, l Điểm F: Giao điểm đường của h, l Điểm I: Trung điểm của m Điểm I: Trung điểm của m Điểm I: Trung điểm của m Điểm D: Giao điểm đường của s, q Điểm D: Giao điểm đường của s, q
a) Do EM = EH và AE vuông góc MH tại E nên AB là đường trung trực của MH. Tương tự AC là trung trực HN.
b) Do AB là đường trung trực của MH nên AM = AH. Tương tự AH = AN
Vậy AM = AN hay tam giác AMN cân tại A.
c) Xét tam giác HMN có E, F lần lượt là trung điểm HM, HN nên EF là đường trung bình tam giác.
Vậy EF // MN.
d) Tam giác cân AMN có I là trung điểm MN nên \(AI⊥MN\)
Lại có MN //EF nên \(AI⊥EF.\)

a) Ta thấy AB vuông góc với MH tại trung điểm E của MH nên AB là đường trung trực của MH.
Ta thấy AC vuông góc với NH tại trung điểm F của NH nên AC là đường trung trực của NH.
b) Do AB là trung trực của MH nên AM = AH.
Tương tự AN = AH. Vậy nên AM = AN hay tam giác AMN cân tại A.
c) Xét tam giác HMN có E là trung điểm MH, F là trung điểm HN nên EF là đường trung bình tam giác HMN.
Suy ra EF // MN.
d) Do tam giác AMN cân tại A nên trung tuyến AI đồng thời là đường cao. Vậy AI vuông góc MN.
Lại có MN // EF nên AI vuông góc EF.

xét 2 tam giác MBE và tam giác HBE =
=> MB=HB
xét 2 tam giác AME = tam giác AHE
=> AM=HA
xét 2 tam giác BMA và tam giác BHA có
BA chung
BM=BH
MA=MH
=> 2 tam giác =
mà góc BHA vuông góc
=> BMA vuông góc
=> BM vuông góc với AM
câu b thì mình vẽ nó song song cơ... gửi cho mình cái hình nha

Gọi giao điểm HM với DC là P; giao điểm HN với BC là E
a) Vì HP vuông góc với IK, mà IK//CD nên DC vuông góc với HP
=> HP và CE là các đường cao của ▲HCN cắt nhau ở M
=> M là trực tâm ▲HCN , nên NM là đường cao thứ 3 hay NM vuông góc với HC
Lại có HC vuông góc với AB (CH là đường cao)
=> NM//AB
Xét ▲BDC có M là trung điểm BC và NM//BD nên ND = NC
b) Do IK//CD nên theo Talet: IH/DN = IK/NC (= AI/AN)
=> IH/IK = ND/NC = 1 (Vì ND = NC). Vậy IH = HK
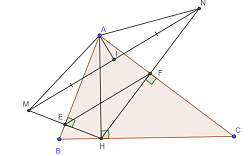
A B C H E M F N
a/ Ta có : AE là cạnh chung của hai tam giác vuông: tam giác AME và tam giác AHE ; ME = EM (gt)
=> tam giác AME = tam giác AHE (2 cạnh góc vuông)
b/ Dễ thấy EH = EM ; AB vuông góc MH => đpcm
Tương tự với AC .
c/ Ta chứng minh được : AB là đường trung trực của MH
=> AM = AH (1)
AC là đường trung trực của NH => AH = AN (2)
Từ (1) và (2) suy ra AM = AN => tam giác AMN cân tại A
d/ Hãy chứng minh MN // EF