Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

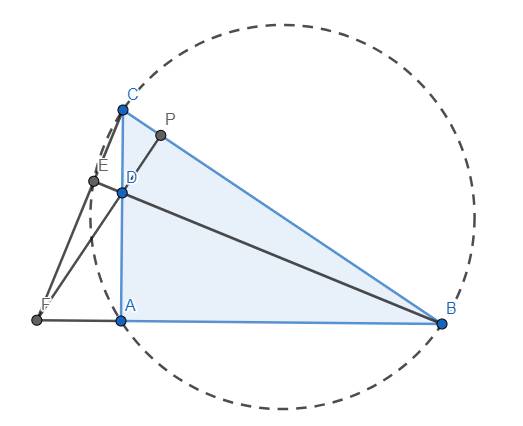
a) Ta có \(\widehat{CEB}=\widehat{CAB}=90^o\) nên 4 điểm A, B, C, E cùng thuộc đường tròn đường kính BC.
b) Kẻ \(FP\perp BC\) tại P. Ta thấy D là trực tâm tam giác FBC nên \(P\in DF\). Dễ thấy \(\Delta CDP~\Delta CBA\left(g.g\right)\) \(\Rightarrow\dfrac{CD}{CB}=\dfrac{CP}{CA}\) \(\Rightarrow CD.CA=CB.CP\)
CMTT, ta có \(BD.BE=BC.BP\)
Do đó \(CD.CA+BD.BE=CB.CP+BC.BP\) \(=BC\left(CP+BP\right)\) \(=BC^2\). Vậy đẳng thức được chứng minh.

trong tam giac vuong ABH Cco \(AH^2+BH^2=AB^2\Rightarrow AH^2=AB^2-BH^2\left(1\right)\)
AHC co \(AH^2+HC^2=AC^2\Rightarrow AH^2=AC^2-HC^2\left(2\right)\)
tu (1) va(2 ) suy ra \(AB^2-BH^2=AC^2-HC^2\Rightarrow AB^2+HC^2=AC^2+BH^2\)

a, Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=\sqrt{32}=4\sqrt{2}\)cm
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{16}{4\sqrt{2}}=\dfrac{4}{\sqrt{2}}=\dfrac{4\sqrt{2}}{2}=2\sqrt{2}\)cm
* Áp dụng hệ thức :\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{16}{4\sqrt{2}}=\dfrac{4}{\sqrt{2}}=2\sqrt{2}\)cm
-> HC = BC - HB = 4\(\sqrt{2}\)- 2\(\sqrt{2}\) = 2 \(\sqrt{2}\)
sinB = \(\dfrac{AC}{BC}=\dfrac{4}{4\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
cosB = \(\dfrac{AB}{BC}=\dfrac{4}{4\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
tanB = \(\dfrac{AC}{AB}=\dfrac{4}{4}=1\)
cotaB = \(\dfrac{AB}{AC}=\dfrac{4}{4}=1\)
tương tự với tỉ số lượng giác ^C
b, bạn cần cm cái gì ? ;-;
b: Xét tứ giác AEHD có
\(\widehat{EAD}=\widehat{AEH}=\widehat{ADH}=90^0\)
Do đó: AEHD là hình chữ nhật
Xét ΔAHB vuông tại H có HD là đường cao ứng với cạnh huyền AB
nên \(BD\cdot DA=DH^2\)
Xét ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC
nên \(CE\cdot EA=EH^2\)
Xét ΔEHD vuông tại H, ta được:
\(ED^2=EH^2+HD^2\)
hay \(ED^2=DA\cdot DB+EA\cdot EC\)