
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo hệ quả định lí cosin, ta có cos A ^ = A B 2 + A C 2 − B C 2 2 A B . A C = 5 2 + 8 2 − 7 2 2.5.8 = 1 2 .
Do đó, A ^ = 60 ° .
Chọn C.

Cho \(\Delta ABC\)có AB = 8, BC = 17 , AC = 15. Số đo góc A = ?
Theo định lí Pytago, nếu AB2 + AC2 = BC2 thì tam giác đó là tam giác vuông
Thay AB = 8, BC = 17, AC = 15 ta có
AB2 + AC2 = 82 + 152 = 289
BC2 = 172 = 289
=> 82 + 152 = 172
=> AB2 + AC2 = BC2 ( Đ/lí Pytago )
=> \(\Delta ABC\)là tam giác vuông tại A
=> \(\widehat{A}=90^0\)
Tam giác ABC có :
8²+15²=289; 17²=289
=>AB² +AC²=BC²=>tam giác ABC vuông tại A
(đ/l pytago đảo)
=>Â =90°

a.
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cosA}=7\)
\(S=\dfrac{1}{2}AB.AC.sinA=10\sqrt{3}\)
\(\Rightarrow h_a=\dfrac{2S}{BC}=\dfrac{20\sqrt{3}}{7}\)
\(R=\dfrac{BC}{2sinA}=\dfrac{7\sqrt{3}}{3}\)
b.
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=-\dfrac{11}{34}\)
\(\Rightarrow sinA=\dfrac{3\sqrt{115}}{34}\)
\(S=\dfrac{1}{2}AB.AC.sinA=6\sqrt{115}\)
\(h_a=\dfrac{2S}{BC}=\dfrac{4\sqrt{115}}{7}\)
\(R=\dfrac{BC}{2sinA}=...\)

Áp dụng định lý hàm cos ta có:
\(cosA=\frac{AB^2+AC^2-BC^2}{2AB.AC}=\frac{5^2+8^2-7^2}{2.5.8}=\frac{1}{2}\)
\(\Rightarrow\widehat{A}=60^0\)

\(BC=AB^2+AC^2-2\cdot AB\cdot AC\cdot\cos A=148\left(cm\right)\)

Lời giải:
$\overrightarrow{CM}.\overrightarrow{BN}=(\overrightarrow{CA}+\overrightarrow{AM})(\overrightarrow{BA}+\overrightarrow{AN})$
$=\overrightarrow{CA}.\overrightarrow{BA}+\overrightarrow{CA}.\overrightarrow{AN}+\overrightarrow{AM}.\overrightarrow{BA}+\overrightarrow{AM}.\overrightarrow{AN}$
$=\overrightarrow{AB}.\overrightarrow{AC}+\overrightarrow{CA}.\frac{1}{4}\overrightarrow{AC}+\frac{1}{5}\overrightarrow{AB}.\overrightarrow{BA}+\frac{1}{5}\overrightarrow{AB}.\frac{1}{4}\overrightarrow{AC}$
$=\frac{21}{20}\overrightarrow{AB}.\overrightarrow{AC}-\frac{1}{4}AC^2-\frac{1}{5}AB^2$
$=\frac{21}{20}\cos A.|\overrightarrow{AB}|.|\overrightarrow{AC}|-\frac{1}{4}AC^2-\frac{1}{5}AB^2$
$=\frac{21}{20}.\frac{1}{2}.5.8-\frac{1}{4}.8^2-\frac{1}{5}.5^2=0$
$\Rightarrow CM\perp BN$

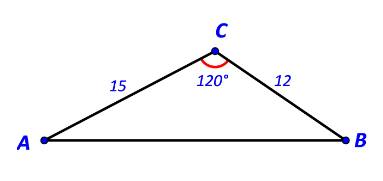
a) Áp dụng định lí cosin trong tam giác ABC ta có:
\(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C\)
\(\begin{array}{l} \Leftrightarrow A{B^2} = {15^2} + {12^2} - 2.15.12.\cos {120^o}\\ \Leftrightarrow A{B^2} = 549\\ \Leftrightarrow AB \approx 23,43\end{array}\)
b) Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}\)
\( \Rightarrow \sin A = \frac{{BC}}{{AB}}.\sin C = \frac{{12}}{{23,43}}.\sin {120^o} \approx 0,44\)
\( \Rightarrow \widehat A \approx {26^o}\) hoặc \(\widehat A \approx {154^o}\) (Loại)
Khi đó: \(\widehat B = {180^o} - ({26^o} + {120^o}) = {34^o}\)
c)
Diện tích tam giác ABC là: \(S = \frac{1}{2}CA.CB.\sin C = \frac{1}{2}.15.12.\sin {120^o} = 45\sqrt 3 \)

\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=\dfrac{5^2+8^2-7^2}{2.5.8}=\dfrac{1}{2}\)
\(\Rightarrow A=60^0\)