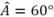Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng BĐT: \(a^2+b^2\ge2ab\Leftrightarrow2a^2+2b^2\ge a^2+2ab+b^2\Leftrightarrow a^2+b^2\ge\frac{\left(a+b\right)^2}{2}\)
\(f\left(x\right)=x^4+\left(1-x\right)^4\ge\frac{\left[x^2+\left(1-x\right)^2\right]^2}{2}\ge\frac{\left[\frac{\left(x+1-x\right)^2}{2}\right]^2}{2}=\frac{1}{8}\)
Dấu "=" xảy ra \(\Leftrightarrow x=1-x\Leftrightarrow x=\frac{1}{2}\)
Vậy tập giá trị của f(x) là: [1/8;+\(\infty\))

Số phần tử của tập hợp A = { k2 + 1 | k εℤ, |k| \(\le\)2} là:
A. 1
B. 2
C. 3
D. 5

a: góc C=90-30=60 độ
Xét ΔBAC vuông tại A có cos B=AB/BC
nên \(BC=\dfrac{2\sqrt{3}}{cos30}=4\left(cm\right)\)
=>AC=2cm
b: Xét ΔbAC vuông tại A có cos B=AB/BC
nên AB/BC=1/2
=>BC=2
=>AC=căn 3

\(\widehat{C}=180^0-\widehat{A}-\widehat{B}=105^0\)
Theo định lý hàm sin:
\(\frac{a}{sinA}=\frac{c}{sinC}\Rightarrow a=\frac{c.sinA}{sinC}=\frac{4.sin30^0}{sin105^0}=2\left(\sqrt{6}-\sqrt{2}\right)\)
Diện tích tam giác:
\(S=\frac{1}{2}ac.sinB=\frac{1}{2}4.2\left(\sqrt{6}-\sqrt{2}\right).sin45^0=2,93\left(cm^2\right)\)
Chọn B.
Theo định lí hàm cosin, ta có
Do đó