Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét tam giác AMB và tam giác DMC có:
BM = CM (gt)
AM =DM (gt)
\(\widehat{AMB}=\widehat{DMC}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AMB=\Delta CMD\left(c-g-c\right)\)
b) Do \(\Delta AMB=\Delta CMD\Rightarrow\widehat{BAM}=\widehat{DCM}\)
Chúng lại ở vị trí so le trong nên AB //CD.
c) Xét tam giác AME có MH là đường cao đồng thời trung tuyến nên tam giác AME cân tại M.
Suy ra MA = ME
Lại có MA = MD nên ME = MD.
d) Xét tam giac AED có MA = ME = MD nê tam giác AED vuông tại E.
Suy ra ED // BC
Xét tam giác cân MED có MK là trung tuyến nên đồng thời là đường cao.
Vậy thì \(MK\perp ED\Rightarrow MK\perp BC\)

a, tam giác ABC vuông tại A (gt) => BC^2 = AC^2 + AB^2 (pytago)
BC = 10; AB = 8 (Gt)
=> AC^2 = 10^2 - 8^2
=> AC^2 = 36
=> AC = 6 do AC > 0
b, xét tam giác AMB và tam giác DMC có : AM = MD (gt)
BM = MC do M là trung điểm của BC(gt)
^BMA = ^DMC (đối đỉnh)
=> tam giác AMB = tam giác DMC (c-g-c)
=> ^ABM = ^MCD mà 2 góc này slt
=> AB // CD
AB _|_ AC
=> CD _|_ AC
c, xét tam giác ACE có : AH _|_ AE
AH = HE
=> tam giác ACE cân tại C
d, xét tam giác BMD và tam giác CMA có L BM = MC
AM = MD
^BMD = ^CMA
=> tam giác BMD = tam giác CMA (c-g-c)
=> BD = AC
AC = CE do tam giác ACE cân tại C (câu c)
=> BD = CE

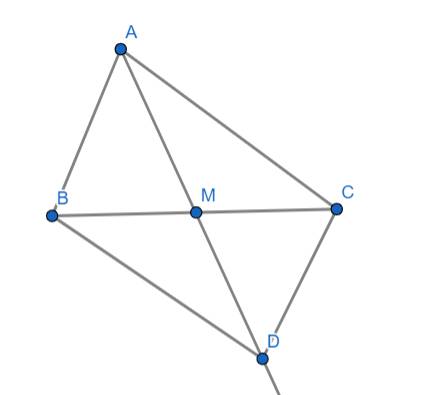
a) Xét ΔAMB và ΔDMC có:
\(AM=CM\) (gt)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
\(BM=CM\) (M là trung điểm của BC)
\(\Rightarrow\text{Δ}AMB=\text{Δ}DMC\left(c.g.c\right)\)
b) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)
\(\Rightarrow AB=DC\) (2 cạnh t.ứng)
c) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)
\(\Rightarrow\widehat{MAB}=\widehat{MDC}\) (hai góc t.ứng)
Mà hai góc này ở vị trí so le trong
\(\Rightarrow AB//CD\)

a) \(\Delta ABC\) vuông tại A áp dụng định lý Py-ta-go ta có:
\(BC=\sqrt{AC^2+AB^2}=\sqrt{15^2-8^2}=17\left(cm\right)\)
b) Xét \(\Delta ABM\) và \(\Delta DMC\) ta có:
\(MA=MD\left(gt\right)\)
\(\widehat{BMA}=\widehat{DMC}\) (hai góc đổi đỉnh)
\(BM=MC\) (M là trung điểm của BC)
\(\Rightarrow\Delta ABM=\Delta DMC\left(c-g-c\right)\)
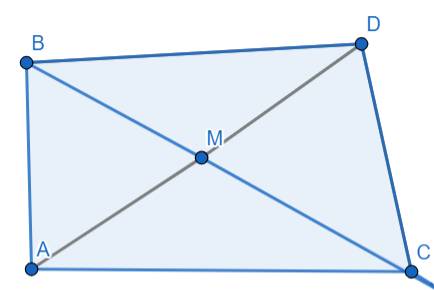

a: Xét ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
Do đo ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
nên ABDC là hình bình hành
=>AC//BD
c: Xét ΔAHB vuông tại H và ΔDKC vuông tại K có
AB=DC
góc ABH=góc DCK
Do đo: ΔAHB=ΔDKC
=>AH=DK và BK=CH

A B C D M
a) Xét ΔAMB và ΔDMC có:
MA=MD(gt)
\(\widehat{AMB}=\widehat{DMC}\left(đđ\right)\)
MB=MC(gt)
=> ΔAMB=ΔDMC(c.g.c)
b)Vì: ΔAMB=ΔDMC(cmt)
=> AB=DC ; \(\widehat{ABC}=\widehat{DCB}\)
Xét ΔABC và ΔDCB có:
BC: cạnh chung
\(\widehat{ABC}=\widehat{DCB}\left(cmt\right)\)
AB=DC(cmt)
=> ΔABC=ΔDCB(c.g.c)
=>AC=BD
\(\widehat{ACB}=\widehat{DBC}\) . Mà hai góc này ở vị trí sole trong
=>AC//BD
Vì: ΔABC=ΔDCB(cmt)
=> \(\widehat{BAC}=\widehat{CDB}=90^o\)

a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: ΔAMB=ΔDMC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
c: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
XétΔCAD có
CM là đường cao
CM là đường trung tuyến
Do đó: ΔCAD cân tại C
Ta có: ΔCAD cân tại C
mà CM là đường cao
nên CM là phân giác của góc ACD
=>CB là phân giác của góc ACD
a,
Xét △ABC có:
BC2 = 172 = 289
AB2 + AC2 = 152 + 82 = 225 + 64 = 289
=> BC2 = AB2 + AC2
=> △ABC vuông