Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác BAH và tam giác CAH, có:
AH: cạnh chung
AB = AC ( tam giác ABC cân tại A )
góc AHB = góc AHC ( = 90 độ )
-> tam giác BAH = tam giác CAH ( ch-cgv )
-> HB = HC ( 2 cạnh tương ứng )
b) Xét tam giác FBH và tam giác ECH, có:
HB = HC ( cmt )
góc D = góc E ( = 90 độ )
góc B = góc C ( tam giác ABC cân tại A )
-> tam giác FBH = tam giác ECH ( ch-gn )
-> HF = HE ( 2 cạnh tương ứng )
-> tam giác HEF là tam giác cân tại H
k cho mình nha mỏi tay quá !!! thanks

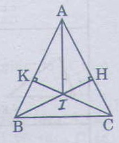
a) Hai tam giác vuông ABH và ACK có:
AB = AC(gt)
Góc A chung.
nên ∆ABH = ∆ACK(Cạnh huyền- Góc nhọn)
suy ra AH = AK.
b) Hai tam giác vuông AIK và AIH có:
AK = AH(cmt)
AI cạnh chung
Nên ∆AIK = ∆AIH(cạnh huyền- cạnh góc vuông)
Suy ra ˆIAKIAK^=ˆIAHIAH^
Vậy AI là tia phân giác của góc A.
a) Hai tam giác vuông ABH và ACH có:
Tam giác ABC cân tại A ⇒ AB = AC
AH cạnh chung.
Nên ∆ABH = ∆ACH(Cạnh huyền – cạnh góc vuông)
Suy ra HB = HC
b)∆ABH = ∆ACH (Câu a)
Suy ra ∠BAH = ∠CAH (Hai góc tương ứng)

Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau

a: Xét ΔACE vuông tạiC và ΔAKE vuông tại K có
AE chung
góc CAE=góc KAE
Do đó: ΔACE=ΔAKE
Suy ra: AC=AK và EC=EK
=>AE là đường trung trực của CK
hay AE\(\perp\)CK
b: Xét ΔEAB có \(\widehat{EAB}=\widehat{EBA}\)
nên ΔEAB cân tại E
mà EK là đường cao
nên K là trung điểm của AB
c: AC=AK=KB
mà EB>KB
nên EB>AC

\(MH\perp AB\left(gt\right)\Rightarrow\widehat{MHA}=\widehat{MHB}=90^0\)
\(MK\perp AC\left(gt\right)\Rightarrow\widehat{MKA}=\widehat{MKC}=90^0\)
M là trung điểm của BC (gt) nên MB = MC
AM là tia phân giác của góc A (gt) \(\Rightarrow\widehat{BAM}=\widehat{CAM}\Rightarrow\widehat{HAM}=\widehat{KAM}\)
\(\Delta AHM=\Delta AKM\left(ch-gn\right)\Rightarrow HM=KM\) (2 cạnh tương ứng)
\(\Delta HMB=\Delta KMC\left(ch-cgv\right)\Rightarrow\widehat{B}=\widehat{C}\) ( 2 góc t/ứ)
Sai đề rồi phải là kẻ \(AH\perp BC\left(H\in BC\right)\) nhé!
A B C H E F
a) Xét 2 Δ vuông: Δ AHB = Δ AHC (c.h-g.n) vì:
\(\hept{\begin{cases}AB=AC\left(gt\right)\\\widehat{ACB}=\widehat{ABC}\left(gt\right)\end{cases}}\)
=> \(BH=HC\)
b) Xét 2 Δ vuông: Δ BHF = Δ CHE (c.h-g.n) vì:
\(\hept{\begin{cases}HB=HC\left(p.a\right)\\\widehat{HBF}=\widehat{HCE}\left(gt\right)\end{cases}}\)
=> \(HE=HF\) => Tam giác HEF cân tại H