Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì tam giác ABC là tam giác cân nên góc B = góc C = (180 độ - 48 độ):2 = 66 độ
Ta có : \(AB=AC=\frac{AH}{sinB}=\frac{13}{sin66^o}\) (cm)
\(BC=2HB=2.\frac{AH}{tanB}=\frac{26}{tan66^o}\) (cm)
Suy ra chu vi tam giác ABC : \(AB+BC+AC=\frac{26}{sin66^o}+\frac{26}{tan66^o}\) (cm)


Áp dụng định lý Pitago:
\(AB=\sqrt{AH^2+BH^2}=\sqrt{41}\)
Áp dụng hệ thức lượng:
\(AB^2=BH.BC\Rightarrow BC=\dfrac{AB^2}{BH}=\dfrac{41}{4}\)
Áp dụng Pitago:
\(AC=\sqrt{BC^2-AB^2}=\dfrac{5\sqrt{41}}{4}\)
Chu vi: \(AB+AC+BC=\dfrac{41+9\sqrt{41}}{4}\left(cm\right)\)

a. + CH = 10 - 3.6 = 6.4 (cm)
- Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông vào ΔABC ta có :
+ \(AH^2=BH.CH\)
\(\Rightarrow AH=\sqrt{BH.CH}=\sqrt{3,6.6,4}=4.8\) (cm)
+ \(AB^2=BC.BH\)
\(\Rightarrow AB=\sqrt{BC.BH}=\sqrt{10.3,6}=6\) (cm)
+ \(AC^2=BC.CH\)
\(\Rightarrow AC=\sqrt{BC.CH}=\sqrt{10.6,4}=8\) (cm)
b. \(S_{ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.6.8=24\left(cm^2\right)\)
c. \(P_{ABC}=AB+AC+BC=6+8+10=24\left(cm\right)\)

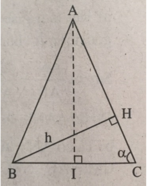
∠ A = 180 ° - 2 α . Tam giác vuông HBC có BC = h/sinα. Kẻ đường cao AI của tam giác ABC thì được
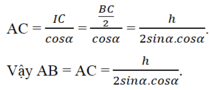

a, AB = 7,5cm, AC = 10cm, BC = 12,5cm, HC = 8cm
b, AH = 3 3 cm; P A B C = 18 + 6 3 c m ; P A B H = 9 + 3 3 c m ; P A C H = 9 + 9 3 c m
BH=CH=2,3 (trong tg cân đường cao đồng thời là đường trung trực) \(\Rightarrow BC=2BH=4,6\)
\(\widehat{BAH}=\widehat{CAH}=\dfrac{\widehat{A}}{2}=25^o\) (trong tg cân đường cao đồng thời là đường phân giác)
\(AB=AC\) (cạnh bên tg cân)
Xét tg vuông ABH có
\(\sin\widehat{BAH}=\dfrac{BH}{AC}\Rightarrow AB=AC=\dfrac{BH}{\sin\widehat{BAH}}=\dfrac{2,3}{\sin25^o}\)
\(C_{ABC}=AB+AC+BC=\dfrac{4,6}{\sin25^o}+4,6\)