MN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
7 tháng 8 2017
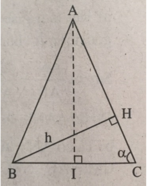
∠ A = 180 ° - 2 α . Tam giác vuông HBC có BC = h/sinα. Kẻ đường cao AI của tam giác ABC thì được
HT
1
KT
1 tháng 8 2018
A B C H 30
Tam giác ABH vuông tại H, có góc ABH = 300
=> góc A = 600
mà tam giác ABC cân tại A
=> tam giác ABC đều
=> góc B = góc C = 600
\(\tan A=\tan60^0=\frac{BH}{AH}=\sqrt{3}\)
=> \(AH=\frac{BH}{\sqrt{3}}=\frac{5}{\sqrt{3}}\)
do tam giác ABC đều, BH là đường cao
=> BH đồng thời là trung tuyến
=> \(AC=\frac{10}{\sqrt{3}}\)
Vậy \(AB=AC=BC=\frac{10}{\sqrt{3}}\); \(\widehat{A}=\widehat{B}=\widehat{C}=60^0\)
4 tháng 8 2016
Câu 1:
Áp dụng đ/lí pytago vào tam giác ABC vuông tại A CÓ:AB^2+AB^2=BC^2
Hay: 12^2+5^2=169=BC^2
=> BC=13cm
ÁP dụng hệ thức ta có:
+) AB^2=BH.BC
Hay: BH=AB^2:BC=144:13 =144/13(cm)
Ta có CH=BC-BH=13-144/13=25/13(cm)
NT
0
22 tháng 9 2015
BÀI 2 : áp dụng hệ thức lượng trong tam giác, ta có: AH^2=BH*CH=>AH^2= 4*9=36=>AH=căn bậc hai của 36=6
\(AB^2=BH\cdot BC=4\cdot\left(4+9\right)=52=>AB=\sqrt{52}=2\sqrt{13}\)
\(AC^2=CH\cdot BC=9\cdot13=117=>AC=\sqrt{117}=3\sqrt{13}\)
H
1
25 tháng 7 2023
AB=căn AH*AC=6(cm)
BC=căn AC^2-AB^2=căn 9^2-6^2=căn 45=3*căn 5(cm)
Xét ΔABC vuông tại B có sin C=AB/AC=6/9=2/3
nên góc C=42 độ
=>góc A=48 độ
25 tháng 12 2020
Giải
- Áp dụng 1 số hệ thức về cạnh và đường cao trong Δ vuông ABC ta có :
\(AH^2=BH.CH\Rightarrow CH=\dfrac{AH^2}{BH}=\dfrac{12^2}{9}=16\left(cm\right)\)
\(\Rightarrow BC=16+9=25\left(cm\right)\)
- Áp dụng định lý Pytago trong \(\Delta AHC\perp H\) ta có :
\(AC=\sqrt{12^2+16^2}=20\left(cm\right)\)
\(\Rightarrow AB=\sqrt{25^2-20^2}=15\left(cm\right)\)
- Áp dụng tỉ số lượng giác của góc nhọn trong Δ vuông \(ABC\) ta có :
+ \(\tan C=\dfrac{AB}{AC}=\dfrac{15}{20}=\dfrac{3}{4}\)
\(\Rightarrow\) Góc \(C\approx37\) độ
\(\Rightarrow\) Góc CAH = Góc B = 53 độ
\(\Rightarrow\) Góc BAH = 37 độ