Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

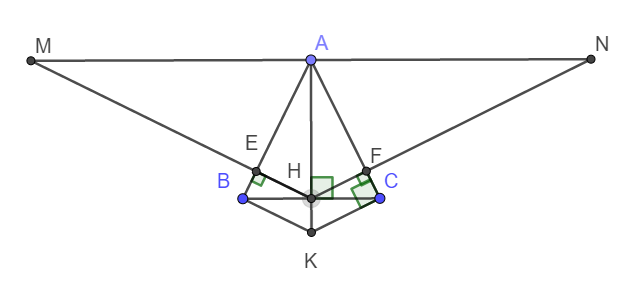
a) Xét tam giác vuông ABH và tam giác vuông ACH có:
Cạnh AH chung
AB = AC (gt)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\) (Hai góc tương ứng)
Vậy nên AH là tia phân giác góc BAC.
b) Xét hai tam giác vuông AEH và AFH có:
Cạnh AH chung
\(\widehat{EAH}=\widehat{FAH}\)
\(\Rightarrow\Delta AEH=\Delta AFH\) (Cạnh huyền - góc nhọn)
\(\Rightarrow HE=HF\) (Hai cạnh tương ứng)
Suy ra tam giác HEF cân tại E.
c) Dễ thấy \(\Delta ABK=\Delta ACK\left(c-g-c\right)\)
\(\Rightarrow\widehat{AKB}=\widehat{AKC}\)
Lại có \(\widehat{AKC}=\widehat{AHF}\) (Đồng vị)
\(\widehat{AHF}=\widehat{AHE}\) (Do \(\Delta AEH=\Delta AFH\) )
\(\Rightarrow\widehat{AKB}=\widehat{AHE}\) hay HE // BK
d) Ta có \(\Delta AHN=\Delta AHM\left(c-g-c\right)\)
\(\Rightarrow\widehat{MAH}=\widehat{NAH}=90^o\)
\(\Rightarrow\widehat{MAN}=180^o\) hay M, N, A thẳng hàng.

1. Xét hai tam giác vuông ΔABHΔABH và ΔACHΔACH có:
AHAH cạnh chung
AB=AC=10cmAB=AC=10cm (gt)
Vậy ΔABH=ΔACHΔABH=ΔACH (cạnh huyền- cạnh góc vuông)
HC=HBHC=HB (hai cạnh tương ứng) hay H là trung điểm BC
2. BH=HC=BC2=122=6BH=HC=BC2=122=6 cm
Áp dụng định lí Py-ta-go vào ΔΔ vuông ABHABH có:
AH2=AB2−HB2=102−62=64⇒AH=8AH2=AB2−HB2=102−62=64⇒AH=8 cm
3. Xét ΔAKEΔAKE và ΔAKHΔAKH có:
AKAK chung
ˆAKE=ˆAKH=90oAKE^=AKH^=90o (do HK⊥ACHK⊥AC)
KE=KHKE=KH (do giả thiết cho K là trung điểm của HE)
⇒ΔAKE=ΔAKH⇒ΔAKE=ΔAKH (c.g.c)
⇒AE=AH⇒AE=AH (hai cạnh tương ứng) (1)
Cách khác để chứng minh AE=AH
Do ΔAHEΔAHE có K là trung điểm của HE nên AK là đường trung tuyến,
Có HK⊥ACHK⊥AC hay AK⊥HEAK⊥HE nên AK là đường cao
ΔAHEΔAHE có AK là đường trung tuyến cũng là đường cao nên ΔAHEΔAHE cân đỉnh A nên AE=AH.
4. Ta có HI⊥ABHI⊥AB hay AI⊥DH⇒AI⊥DH⇒ AI là đường cao của ΔADHΔADH
Mà IH=ID nên AI cũng là đường trung tuyến ΔADHΔADH
Vậy ΔAEHΔAEH cân tại A
Nên AD=AH (2)
Từ (1) và (2) suy ra AE=AD hay ΔAEDΔAED cân tại A.
5. Xét 2 tam giác vuông ΔAHIΔAHI và ΔAHKΔAHK có:
AH chung
ˆIAH=ˆKAHIAH^=KAH^ (hai góc tương ứng của ΔABH=ΔACHΔABH=ΔACH)
⇒ΔAHI=ΔAHK⇒ΔAHI=ΔAHK (cạnh huyền- góc nhọn)
⇒HI=HK⇒2HI=2HK⇒HD=HE⇒HI=HK⇒2HI=2HK⇒HD=HE
Mà ta có AD=AEAD=AE (cmt)
⇒AH⇒AH là đường trung trực của DE⇒AH⊥DEDE⇒AH⊥DE mà AH⊥BCAH⊥BC
⇒DE//BC⇒DE//BC
6. Để A là trung điểm ED thì DA⊥AHDA⊥AH mà ΔADHΔADH cân (cmt) nên ΔADHΔADH vuông cân đỉnh A.
Có AIAI là đường cao, đường trung tuyến nên AIAI cũng là đường phân giác nên
ˆDAI=ˆHAI=90o2=45oDAI^=HAI^=90o2=45o
⇒ˆIAH=ˆBAH=ˆCAH=45o⇒IAH^=BAH^=CAH^=45o (do ΔABH=ΔACHΔABH=ΔACH)
⇒ˆBAC=ˆBAH+ˆCAH=90o⇒BAC^=BAH^+CAH^=90o và ΔABCΔABC cân đỉnh A
⇒ΔABC⇒ΔABC vuông cân đỉnh A.
Vậy nếu ΔABCΔABC vuông cân đỉnh A thì AA là trung điểm của DE.





a) vì tam giác ABC cân tại A nên góc B = góc C = 65độ(2 góc tương ứng )
ta có : gócA + gócB + gócC = 180độ( tổng 3 góc 1 tam giác )
gócA + 65độ + 65độ = 180độ
=>gócA = 180 - 65 - 65 =50
b)xét tam giác ABH và tam giác ACH , có :
gócB = gócC
AB = AC
=>tam giác ABH = tam giác ACH (cạnh huyền - góc nhọn )
câu c tui ko biết làm