Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔiAB và ΔICD có
IA=IC
góc AIB=góc CID
IB=ID
=>ΔIAB=ΔICD
b: Xét ΔBAC có
BI,AM là trung tuyến
BI cắt AM tại G
=>G là trọng tâm
=>BG=2/3BI=2/3ID
c: Xét ΔDAC có
DI,AN là trung tuyến
DI cắt AN tại K
=>K là trọng tâm
=>DK=2/3DI=2/3*1/2*DB=1/3DB
BG=2/3BI
=>BG=2/3*1/2BD=1/3BD
BG+GK+KD=BD
=>GK=1/3BD=DK=BG

I A B C D E M 1 2 2 1
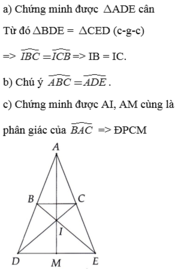
a) Vì AB = AC (do \(\Delta ABC\) cân tại A)
BD = CE (gt)
=> AD = AE
Xét hai tam giác ABE và ACD có:
AB = AC (do \(\Delta ABC\) cân tại A)
\(\widehat{A}\): góc chung
AD = AE (cmt)
Vậy: \(\Delta ABE=\Delta ACD\left(c-g-c\right)\)
Suy ra: BE = CD (hai cạnh tương ứng) (1)
\(\widehat{ABE}=\widehat{ACD}\) (hai góc tương ứng) (2)
\(\Delta ABC\) cân tại A nên \(\widehat{B_1}=\widehat{C_1}\) (3)
Từ (2) và (3) suy ra:
\(\widehat{ABE}-\widehat{B_1}=\widehat{ACD}-\widehat{C_1}\) hay \(\widehat{B_2}=\widehat{C_2}\)
Vậy \(\Delta BIC\) cân tại I, suy ra: IB = IC (4)
Từ (1) và (4) suy ra:
BE - IB = CD - IC hay IE = ID
b) Các tam giác cân ABC và ADE có chung góc ở đỉnh A nên \(\widehat{B_1}=\widehat{ADE}\) (hai góc đồng vị)
Do đó: BC // DE
c) Xét hai tam giác BIM và CIM có:
MB = MC (gt)
\(\widehat{B_2}=\widehat{C_2}\)(cmt)
IB = IC (do \(\Delta BIC\) cân tại I)
Vậy: \(\Delta BIM=\Delta CIM\left(c-g-c\right)\)
Suy ra: \(\widehat{IMB}=\widehat{IMC}\) (hai góc tương ứng)
Mà \(\widehat{IMB}+\widehat{IMC}=180^o\) (kề bù)
Nên \(\widehat{IMB}=\widehat{IMC}\) = 90o (1)
Ta lại có: \(\widehat{IMB}+\widehat{AMB}=180^o\) (kề bù)
Mà \(\widehat{IMB}=90^o\)
\(\Rightarrow\widehat{AMB}=90^o\) (2)
Từ (1) và (2) suy ra: ba điểm A, M, I thẳng hàng (đpcm).

a, xét t.giác AMB và t.giác DMC có:
AM=DM(gt)
\(\widehat{AMB}\)=\(\widehat{DMC}\)(vì đối đỉnh)
CM=BM(gt)
=>t.giác AMB=t.giác DMC(c.g.c)
b,đề bài bị thiếu

a. Xét tam giác ABM và tam giác DCM có:
+, BM = MC ( AM là đường trung tuyến của tam giác ABC )
+, Góc AMB = góc DMC ( 2 góc đối đỉnh )
+, AM = MD ( gt )
=> tam giác ABM = tam giác DCM ( c.g.c )
=> AB = CD ( 2 cạnh tương ứng )
=> góc BAM = góc CDM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong
=> AB // CD ( đpcm )
a: Xét ΔABM và ΔACM có
AB=AC
góc BAM=góc CAM
AM chung
=>ΔABM=ΔACM
=>MB=MC
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
=>ABCD là hình bình hành
=>AB//CD