Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

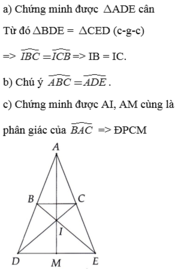
a, đơn giản ta CM được hai tam giác DCB và EBC bằng nhau => góc EBC = góc DCB => tam giác BIC cân tại I => IB = IC (đpcm)
tương tự chứng minh được hai tam giác DIB và EIC bằng nhau => ID = IE (đpcm)
b, ta có tam giác DAE cân tại A => 2góc D = 180o -góc A
tam giác BAC cân tại A => 2 góc B = 180o - góc A
=> góc D = góc B => BC// DE (đpcm)
c, Nối AM => AM vừa là trung tuyến vừa là đường trung trựctại M của BC
Nối IM => IM vừ là trung tuyến vừa là đường trung trực tại M của BC
=> AM và IM cùng nằm trên đường trung trực của BC tại M hay 3 điểm A,M,I thẳng hàng
a) Tam giác ABC cân tại A suy ra \(\widehat{B_1}=\widehat{C_1}\)
Xét tam giác ABM và tam giác ACM có :
AB = AC ( tam giác ABC cân tại A )
\(\widehat{B_1}=\widehat{C_1}\left(cmt\right)\)
BM = CM ( gt )
\(\Rightarrow\Delta ABM=\Delta ACM\left(c-g-c\right)\)
\(\Rightarrow\widehat{A_1}=\widehat{A_2}\)
Xét tam giác ABI và tam giác ACI có :
AI chung
AB = AC ( tam giác ABC cân tại A )
\(\widehat{A_1}=\widehat{A_2}\left(cmt\right)\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c-g-c\right)\)
\(\Rightarrow IB=IC\)
Vì AD = AB + BD
AE = AC + BC
Mà AB = AC ( tam giác ABC cân tại A )
DB = EC ( gt )
\(\Rightarrow AD=AE\)
Xét tam giác ADI và tam giác AEI có :
AI chung
AD = AE ( cmt )
\(\widehat{A_1}=\widehat{A_2}\left(cmt\right)\)
\(\Rightarrow\Delta ADI=\Delta AEI\left(c-g-c\right)\)
\(\Rightarrow DI=EI\)hay ID = IE
b) Vì tam giác ABC cân tại A ( gt )
\(\Rightarrow\)\(\widehat{B_1}=\frac{180^o-\widehat{A}}{2}\left(1\right)\)
Vì tam giác ADE có AD = AE ( cmt )
Suy ra tam giác ADE cân
\(\Rightarrow\widehat{D}=\frac{180^o-\widehat{A}}{2}\left(2\right)\)
Từ ( 1 ) và ( 2 ) suy ra \(\widehat{B_1}=\widehat{D}\)mà hai góc này ở vị trí đồng vị
Suy ra BC // DE
c) Ta có : \(\widehat{M_2}=\widehat{M_1}\left(\Delta ABM=\Delta ACM\right)\left(cmt\right)\)
Mà \(\widehat{M_1}+\widehat{M_2}=180^o\)( 2 góc này ở vị trí kề bù )
\(\widehat{M_2}=\widehat{M_3}\)( đối đỉnh )
\(\Rightarrow\widehat{M_1}+\widehat{M_3}=180^o\)
\(\Rightarrow\)A ; M ; I thẳng hàng

I A B C D E M 1 2 2 1
a) Vì AB = AC (do \(\Delta ABC\) cân tại A)
BD = CE (gt)
=> AD = AE
Xét hai tam giác ABE và ACD có:
AB = AC (do \(\Delta ABC\) cân tại A)
\(\widehat{A}\): góc chung
AD = AE (cmt)
Vậy: \(\Delta ABE=\Delta ACD\left(c-g-c\right)\)
Suy ra: BE = CD (hai cạnh tương ứng) (1)
\(\widehat{ABE}=\widehat{ACD}\) (hai góc tương ứng) (2)
\(\Delta ABC\) cân tại A nên \(\widehat{B_1}=\widehat{C_1}\) (3)
Từ (2) và (3) suy ra:
\(\widehat{ABE}-\widehat{B_1}=\widehat{ACD}-\widehat{C_1}\) hay \(\widehat{B_2}=\widehat{C_2}\)
Vậy \(\Delta BIC\) cân tại I, suy ra: IB = IC (4)
Từ (1) và (4) suy ra:
BE - IB = CD - IC hay IE = ID
b) Các tam giác cân ABC và ADE có chung góc ở đỉnh A nên \(\widehat{B_1}=\widehat{ADE}\) (hai góc đồng vị)
Do đó: BC // DE
c) Xét hai tam giác BIM và CIM có:
MB = MC (gt)
\(\widehat{B_2}=\widehat{C_2}\)(cmt)
IB = IC (do \(\Delta BIC\) cân tại I)
Vậy: \(\Delta BIM=\Delta CIM\left(c-g-c\right)\)
Suy ra: \(\widehat{IMB}=\widehat{IMC}\) (hai góc tương ứng)
Mà \(\widehat{IMB}+\widehat{IMC}=180^o\) (kề bù)
Nên \(\widehat{IMB}=\widehat{IMC}\) = 90o (1)
Ta lại có: \(\widehat{IMB}+\widehat{AMB}=180^o\) (kề bù)
Mà \(\widehat{IMB}=90^o\)
\(\Rightarrow\widehat{AMB}=90^o\) (2)
Từ (1) và (2) suy ra: ba điểm A, M, I thẳng hàng (đpcm).

Tham khảo nhá cậu :)
h.vn/hoi-dap/question/271414.html
Vào thống kê mình khác thấy ((:

Nối D với E
Ta có tam giác ADE cân vì ....
=> góc ADE = góc AED = (180-góc A )/2
mà góc ABC= góc ACB = (180-góc A)/2
=> góc ABC = ADE
maf hai góc này ơr vị trí ĐV của BC và DE
=> BC//DE
tuwf đấy suy ra hai góc bằng nhau và xét tam giác BID và CIE rồi suy ra hai góc tương ứng

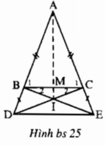
+)Theo giả thiết ta có: AB = AC và BD = CE nên:
AB + BD = AC + CE hay AD = AE.
+) Xét ΔABE và ΔACD có:
AB = AC (gt)
∠A chung
AE = AD (chứng minh trên)
⇒ ΔABE = ΔACD (c.g.c)
⇒ BE = CD (2 cạnh tương ứng) (1)
và ∠ABE = ∠ACD (2 góc tương ứng) (2)
Tam giác ABC cân nên ∠B1 = ∠C1. (3)
Từ (2) và (3) ⇒ ∠ABE - ∠B1 = ∠ACD - ∠C1, tức là ∠B2 = ∠C2.
⇒ ΔBIC cân tại I ⇒ IB = IC. (4)
Từ (1) và (4) suy ra BE - IB = CD – IC, tức là IE = ID.