Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a: \(BC=\sqrt{8^2+6^2}=10\left(cm\right)\)
b: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
c: \(BC=\sqrt{5^2+12^2}=13\left(cm\right)\)

Ta có: 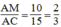
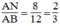
Suy ra: 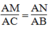
Xét ΔABC và ΔANM, ta có
+ Góc A chung
+ 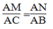
Suy ra:
△
ANM đồng dạng
△
ABC(c.g.c) ⇒ 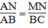
Vậy MN = 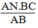 = (8.18)/12 = 12 cm
= (8.18)/12 = 12 cm

a, Ta có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{6}{8}=\dfrac{7,5}{10}=\dfrac{3}{4}\)
=> MN // BC (Ta lét đảo)
b, Vì MN // BC
Theo hệ quả Ta lét \(\dfrac{AM}{AB}=\dfrac{MN}{BC}\Leftrightarrow\dfrac{6}{8}=\dfrac{MN}{12}\Leftrightarrow MN=9cm\)

A B C D E F 5 7 8 12 45 55
Giải
Vì\(\Delta ABC~\Delta DEF\) nên ta có:
\(\widehat{D}=\widehat{A}=45^o\)
\(\widehat{E}=\widehat{B}=55^o\)
\(\widehat{F}=\widehat{C}=\left(180^o-45^o-55^o\right)=80^o\)
Xét\(\Delta ABC~\Delta DEF\) có:
\(\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}=\frac{2}{3}\)
\(\Rightarrow DE=\frac{AB.3}{2}=7,5\)
\(DF=\frac{AC.3}{2}=10,5\)
#hoktot<3#

a: Ta có: ΔA'B'C'∼ΔABC
nên A'B'/AB=B'C'/BC=A'C'/AC
=>A'B'/6=B'C'/12=A'C'/8=3/2
=>A'B'=9cm; B'C'=18cm; A'C'=12cm
b: Ta có: ΔA'B'C'∼ΔABC
nên \(\dfrac{C_{A'B'C'}}{C_{ABC}}=\dfrac{3}{2}\)


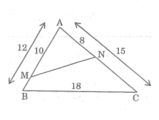
a) Ta có:
\(\frac{{AE}}{{AC}} = \frac{{10}}{{15}} = \frac{2}{3};\frac{{AF}}{{AB}} = \frac{8}{{12}} = \frac{2}{3}\)
Xét tam giác \(AFE\) và tam giác \(ABC\) ta có:
\(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}} = \frac{2}{3}\)
\(\widehat A\) chung
Do đó, \(\Delta AFE\backsim\Delta ABC\) (c.g.c)
Do đó, \(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}} = \frac{{EF}}{{BC}} = \frac{2}{3}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Do đó, \(\frac{{EF}}{{BC}} = \frac{2}{3} \Rightarrow EF = \frac{{BC.2}}{3} = \frac{{18.2}}{3} = 12\)
Vậy \(BC = 12cm\).
b) Vì \(FC = FD\) nên tam giác \(FDC\) cân tại \(F\).
Suy ra, \(\widehat {FDC} = \widehat {FCD}\) (tính chất)
Ta có:
\(\frac{{AC}}{{MD}} = \frac{{15}}{{20}} = \frac{3}{4};\frac{{BC}}{{DE}} = \frac{9}{{12}} = \frac{3}{4}\)
Xét tam giác \(ABC\) và tam giác \(MED\) ta có:
\(\frac{{AC}}{{MD}} = \frac{{BC}}{{DE}} = \frac{3}{4}\)
\(\widehat {FCD} = \widehat {FDC}\) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta MED\) (c.g.c).

Lời giải:
Kẻ $AH\perp BC$. $(H\in BC)$
Xét tam giác $ABH$ có:
$\frac{BH}{AB}=\cos 60^0=\frac{1}{2}$
$\Rightarrow AB=2BH$
Áp dụng định lý Pitago:
$AH^2=AB^2-BH^2=(2BH)^2-BH^2=3BH^2(1)$
$AH^2=AC^2-CH^2=(12-AB)^2-(8-BH)^2$
$=(12-2BH)^2-(8-BH)^2=3BH^2-32BH+80(2)$
Từ $(1);(2)$ suy ra $3BH^2=3BH^2-32BH+80$
$\Rightarrow BH=2,5$ (cm)
$\Rightarrow AB=2BH=5$ (cm)
Hình vẽ: