Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác \(ABD\) và tam giác \(ACB\) có:
\(\widehat {ABD} = \widehat {ACB}\) (giả thuyết)
\(\widehat A\) chung
Suy ra, \(\Delta ABD\backsim\Delta ACB\) (g.g)
b) Vì \(\Delta ABD\backsim\Delta ACB\)
Suy ra, \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Suy ra, \(A{B^2} = AC.AD = 9.4 = 36 \Rightarrow AB = \sqrt {36} = 6\)
Vậy \(AB = 6cm.\)

Tự vẽ hình.
a) Xét tam giác OAB có AB // CD
⇒AOOC=OBOD=ABDC⇒12OC=93=18DC⇒AOOC=OBOD=ABDC⇒12OC=93=18DC ( Hệ quả định lý Ta - lét ) (1)
=> OC = 4cm, DC = 6cm
Vậy OC = 4cm và DC = 6cm
b) Xét tam giác FAB có DC // AB
⇒FDAD=FCCB⇒FD.BC=FC.AD⇒FDAD=FCCB⇒FD.BC=FC.AD ( ĐPCM )
c) Theo (1), ta đã có:
OAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBDOAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBD (2)
Vì MN // AB mà AB // DC => MN // DC
Xét tam giác ADC có MO// DC
⇒MODC=AOAC⇒MODC=AOAC ( Hệ quả định lý Ta - lét ) (3)
CMTT : ONDC=OBDBONDC=OBDB (4)
Từ (2), (3) và (4) => MODC=NODC⇒MO=NOMODC=NODC⇒MO=NO ( ĐPCM )

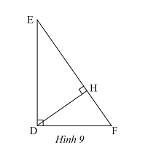
a) Xét \(\Delta DEF\) và \(\Delta HDF\) có:
\(\widehat F\) chung
\(\widehat {EDF} = \widehat {DHF} = 90^\circ \)
Do đó, \(\Delta DEF\backsim\Delta HDF\) (g.g)
b) Vì \(\Delta DEF\backsim\Delta HDF\) nên \(\frac{{DF}}{{HF}} = \frac{{FE}}{{DF}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
\( \Rightarrow D{F^2} = FH.FE\).
c) Theo câu b ta có:
\(D{F^2} = FH.FE\)
Thay số, \(D{F^2} = 5,4.15 = 81 \Rightarrow DF = \sqrt {81} = 9cm\)
Vậy \(DF = 9cm\).

a, Ta có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{6}{8}=\dfrac{7,5}{10}=\dfrac{3}{4}\)
=> MN // BC (Ta lét đảo)
b, Vì MN // BC
Theo hệ quả Ta lét \(\dfrac{AM}{AB}=\dfrac{MN}{BC}\Leftrightarrow\dfrac{6}{8}=\dfrac{MN}{12}\Leftrightarrow MN=9cm\)

- Có EF // BC => \(\widehat {{\rm{AEF}}} = \widehat {AC{\rm{D}}}\) (2 góc đồng vị) (1)
- Có EF // BD (vì EF // BC)
DE // FB (vì MN // BC)
=> EFBD là hình bình hành
=> \(\widehat {EFB} = \widehat {E{\rm{D}}B}\)
mà \(\widehat {EFB} + \widehat {{\rm{AEF}}} = {180^o}\)
\(\widehat {E{\rm{D}}B} + \widehat {E{\rm{D}}C} = {180^o}\)
=> \(\widehat {AF{\rm{E}}} = \widehat {E{\rm{D}}C}\) (2)
Từ (1) và (2) => ΔAEF ∽ ΔECD (g.g)
Có \(\frac{{AF}}{{E{\rm{D}}}} = \frac{2}{4} = \frac{1}{2}\)
=> Đồng dạng với tỉ số \(\frac{1}{2}\)

Hình bạn tự vẽ ạ.
a, Xét \(\Delta ADE\) và \(\Delta ABC\) có :
\(\dfrac{AD}{AB}=\dfrac{7}{14}=\dfrac{1}{2}\)
\(\dfrac{AE}{AC}=\dfrac{10}{20}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(=\dfrac{1}{2}\right)\)
Mà \(\widehat{A}:chung\)
\(\Rightarrow\Delta ADE\sim\Delta ABC\left(c-g-c\right)\)
b, Ta có : \(\Delta ADE\sim\Delta ABC\left(cmt\right)\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{ED}{BC}\)
hay \(\dfrac{7}{14}=\dfrac{ED}{18}\)
\(\Rightarrow ED=\dfrac{7.18}{14}=9\left(cm\right)\)

a) Áp dụng định lý Thales trong tam giác ABC, ta có:
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\) . Kết hợp với giả thiết ta được \(\dfrac{2}{5}=\dfrac{AE}{7,5}\) \(\Rightarrow AE=3\)
b) Ta thấy \(\dfrac{AE}{AC}=\dfrac{3}{7,5}=\dfrac{2}{5}\) nhưng \(\dfrac{BF}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\ne\dfrac{AE}{AC}\) nên theo định lý Thales đảo, ta không thể có EF//AB.


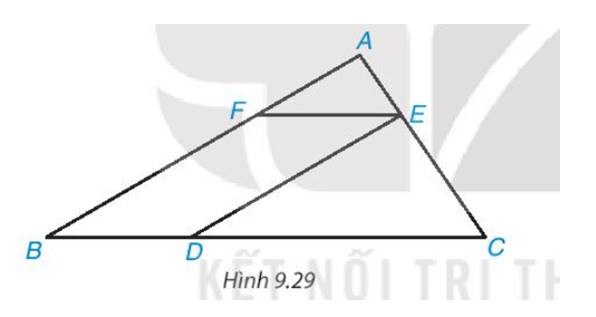
a) Ta có:
\(\frac{{AE}}{{AC}} = \frac{{10}}{{15}} = \frac{2}{3};\frac{{AF}}{{AB}} = \frac{8}{{12}} = \frac{2}{3}\)
Xét tam giác \(AFE\) và tam giác \(ABC\) ta có:
\(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}} = \frac{2}{3}\)
\(\widehat A\) chung
Do đó, \(\Delta AFE\backsim\Delta ABC\) (c.g.c)
Do đó, \(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}} = \frac{{EF}}{{BC}} = \frac{2}{3}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Do đó, \(\frac{{EF}}{{BC}} = \frac{2}{3} \Rightarrow EF = \frac{{BC.2}}{3} = \frac{{18.2}}{3} = 12\)
Vậy \(BC = 12cm\).
b) Vì \(FC = FD\) nên tam giác \(FDC\) cân tại \(F\).
Suy ra, \(\widehat {FDC} = \widehat {FCD}\) (tính chất)
Ta có:
\(\frac{{AC}}{{MD}} = \frac{{15}}{{20}} = \frac{3}{4};\frac{{BC}}{{DE}} = \frac{9}{{12}} = \frac{3}{4}\)
Xét tam giác \(ABC\) và tam giác \(MED\) ta có:
\(\frac{{AC}}{{MD}} = \frac{{BC}}{{DE}} = \frac{3}{4}\)
\(\widehat {FCD} = \widehat {FDC}\) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta MED\) (c.g.c).