Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

C A B D E I H M G K
a) Xét tam giác vuông ECA và EDA có:
Cạnh EA chung
CA = DA (gt)
\(\Rightarrow\Delta ECA=\Delta EDA\) (Cạnh huyền, cạnh góc vuông)
\(\Rightarrow\widehat{CAE}=\widehat{DAE}\) (Hai cạnh tương ứng)
Hya AE là phân giác góc CAB.
b) Theo câu a, \(\Delta ECA=\Delta EDA\Rightarrow EC=ED\)
Ta có EC = ED; AC = AD nên AE là trung trực của CD.
c) Kẻ CH vuông góc AB.
Ta luôn có D nằm giữa B và H nên HD < HB
Vậy thì CD < CB (Quan hệ đường xiên hình chiếu)
d) Ta có I là trung điểm của CD; M là trung điểm của BC nên DM, BI là các đường trung tuyến của tam giác BCD.
Vậy G là trọng tâm hay CK cũng có trung tuyến.
Vậy K là trung điểm BD.

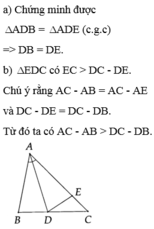
a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
Do đó: ΔABD=ΔAED
=>DB=DE
b: Xét ΔDBF và ΔDEC có
góc DBF=góc DEC
DB=DE
góc BDF=góc EDC
Do đo: ΔDBF=ΔDEC
c:ΔDBF=ΔDEC
nên góc BDF=góc EDC
=>góc BDF+góc BDE=180 độ
=>E,D,F thẳng hàng

A B C D E
a, xét tam giác ABD và tam giác AED có AB = AE (Gt)
AD chung
^BAD = ^EAD do AD Là pg của ^BAC (Gt)
=> tg ABD = tg AED (c-g-c)
=> BD = ED (Đn)
=> tam giác BED cân tại D (đn)
b, tg ABC có AD là pg => DC/AC = DB/AB (tc)
có AC > AB (GT)
=> DC > DB
Bài làm
a) Xét tam giác ADB và tam giác ADE có:
AB = AE ( gt )
\(\widehat{BAD}=\widehat{EAD}\)( Do AD phân giác )
AD chung
=> Tam giác ADB = tam giác ADE ( c.g.c )
=> BD = DE
=> Tam giác DBE cân ở D.
b) Kẻ BH là tia đối của tia BA.
Xét tam giác BAC có: \(\widehat{CBH}=\widehat{BAC}+\widehat{ACB}\)
=> \(\widehat{ACB}< \widehat{CBH}\)
Hay \(\widehat{DCE}< \widehat{CBH}\) (1)
Vì tam giác ADB = tam giác ADE ( cmt )
=> \(\widehat{ABD}=\widehat{AED}\)
Mà \(\widehat{ABD}+\widehat{DBH}=180^0\)( Hai góc kề bù )
\(\widehat{AED}+\widehat{DEC}=180^0\)( Hai góc kề bù )
=> \(\widehat{DBH}=\widehat{DEC}\)
Hay \(\widehat{CBH}=\widehat{DEC}\) (2)
Từ (1) và (2) => \(\widehat{DCE}< \widehat{DEC}\)
Xét tam giác DEC có:
\(\widehat{DCE}< \widehat{DEC}\)
=> DE < DC ( Qua hệ giữ cạnh và góc đối diện )
Mà DE = BD ( cmt )
=> BD < DC
Hay DC > DB ( đpcm )

A B C D E O H
Cm: a) Xét t/giác ABE và t/giác ACD
có: AB = AC (gt)
\(\widehat{A}\) :chung
AE = AD (gt)
=> t/giác ABE = t/giác ACD (c.g.c)
=> BE = CD (2 cạnh t/ứng)
b)Ta có: AD + DB = AB
AE + EC = AC
mà AD = AE (gt) ; AB = AC (gt)
=> BD = EC
Ta lại có: \(\widehat{ADC}+\widehat{CDB}=180^0\) (kề bù)
\(\widehat{AEB}+\widehat{BEC}=180^0\)(kề bù)
mà \(\widehat{ADC}=\widehat{AEB}\)(vì t/giác ABE = t/giác ACD)
=> \(\widehat{BDC}=\widehat{BEC}\)
Xét t/giác BOD và t/giác COE
có: \(\widehat{DBO}=\widehat{OCE}\) (vì t/giác ABE = t/giác ACD)
BD = EC (cmt)
\(\widehat{BDO}=\widehat{OEC}\) (cmt)
=> t/giác BOD = t/giác COE (g.c.g)
c) Xét t/giác ABO và t/giác ACO
có: AB = AC (gT)
OB = OC (vì t/giác BOD = t/giác COE)
AO : chung
=> t/giác ABO = t/giác ACO (c.c.c)
=> \(\widehat{BAO}=\widehat{CAO}\) (2 góc t/ứng)
=> AO là tia p/giác của \(\widehat{A}\)
d) Xét t/giác ABH và t/giác ACH
có: AB = AC (gt)
\(\widehat{BAH}=\widehat{CAH}\)(cmt)
AH : chung
=> t/giác ABH = t/giác ACH (c.g.c)
=> \(\widehat{BHA}=\widehat{CHA}\) (2 góc t/ứng)
Mà \(\widehat{BHA}+\widehat{CHA}=180^0\) (kề bù)
=> \(\widehat{BHA}=\widehat{CHA}=90^0\) => AH \(\perp\)BC (Đpcm)

a: Xét ΔCAD và ΔEAD có
AC=AE
\(\widehat{CAD}=\widehat{EAD}\)
AD chung
Do đó: ΔCAD=ΔEAD
Suy ra: CD=ED
b: Xét ΔABC có AD là đường phân giác
nên AB/BD=AC/CD
mà AB>AC
nên BD>CD
Cảm ơn bạn nhé 🤗🤗🤗😁