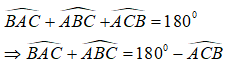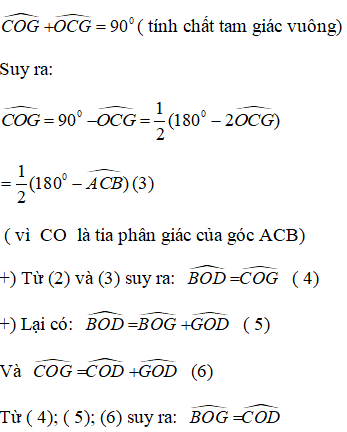Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vẽ hình ra nhé. Mà ^ kí hiệu là góc ha .
Trong tam giác OGC có góc GOC = 90độ trừ ^OCG
hay ^GOC = 90 độ - ^ACB /2 (1)
^BOD là góc ngoài tam giác AOB tại O => ^BOD = ^BAO+^ABO hay ^BOD= ^BAC/2+^ABC/2
=> ^BOD= (180độ - ^ACB) /2 = 90 độ - ^ ACB/2 (2)
Từ (1) và (2) ta có ^GOC=^BOD
Mà ^BOG+ ^GOD = ^BOD
^COD+^DOG =^COG
=> BOG = COD
A B C D E F G O
đÂY LÀ HÌNH Cho tam giác ABC. Vẽ ba đường phân giác AD; BE; CF cắt nhau tại O. Kẻ OG vuông góc BC tại G. Chứng minh rằng góc BOG = góc COD.Mình được gợi ý là dùng góc ngoài. Mình cần cách giải gấp trong một tuần. Giúp mình nhé

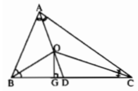
Để chứng minh ∠(BOG) = ∠(COD), ta chứng minh ∠(BOD) = ∠(GOC).
+) Tổng ba góc trong 1 tam giác bằng 180º nên :
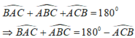
+) Xét tam giác OAB, ta có góc ∠BOD là góc ngoài tam giác tại đỉnh O nên:
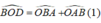
Lại có: BO và AO là tia phân giác của góc B và góc A nên:
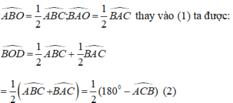
Xét tam giác vuông OCG ta có:
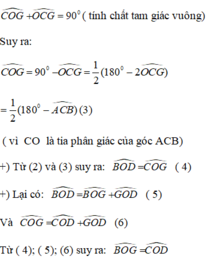

Tham khảo:
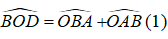
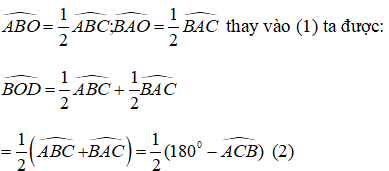

Xét tam giác OAB, ta có
\(\widehat{BOD}=\frac{1}{2}\left(\widehat{A}+\widehat{B}\right)=\frac{1}{2}\left(180^0-\widehat{C}\right)\) (1)
Xét tam giác vuông OCG ta có:
\(\widehat{GOC}=90^0-\frac{1}{2}\widehat{C}=\frac{1}{2}\left(180^0-\widehat{C}\right)\) (2)
Từ (1) và (2) suy ra \(\widehat{BOD}=\widehat{GOC}\)

A B C M N 1 2 2 1 E F 1 1 2 2 O
CM : a) Ta có: t/giác ABC cân tại A
=> góc B2 = góc C2
Mà góc B1 + góc B2 = 1800
góc C1 + góc C2 = 1800
=> góc B1 = góc C1
Xét t/giác AMB và t/giác ANC
có AB = AC (gt)
góc B1 = góc C1 (cmt)
MB = NC (gt)
=> t/giác AMB = t/giác ANC (c.g.c)
=> AM = AN (hai cạnh tương ứng)
=> t/giác AMN là t/giác cân tại A
b) Ta có: t/giác AMN cân tại A
=> góc M = góc N
Xét t/giác BME và t/giác CNF
có góc E1 = góc F1 = 900 (gt)
BM = CN (gt)
góc M = góc N (cmt)
=> t/giác BME = t/giác CNF (cạnh huyền - góc nhọn)
c,d) tự làm