Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Co A B
Vì \(2.\left(-2\right)-3+6=11>0\)
và \(2.1-3\left(-2\right)+6=14>0\) nê A,B cùng phía đối với \(\Delta\). Khi đó mọi \(C\in\Delta\) đều có :
\(\left|CA-CB\right|\le\left|C_0A-C_0B\right|=AB\)
Dấu đẳng thức xảy ra khi và chỉ khi \(C\) trùng với \(C_0\) là giao điểm của đường thẳng AB với \(\Delta\). Do đó tọa độ của điểm C cần tì là nghiệm của hệ phương trình :
\(\begin{cases}2x-3y+6=0\\\frac{x+y}{3}=\frac{y+3}{1}\end{cases}\)
Giải hệ ta được \(\left(x;y\right)=\left(-13;-\frac{20}{3}\right)\) vậy điểm cần tìm là \(C=\left(-13;-\frac{20}{3}\right)\)

a. Gọi I là trung điểm AB khi đó \(I\left(-1;2\right)\) và \(\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\) với mọi M
Do đó \(M\in\Delta\) mà \(\left|\overrightarrow{MA}+\overrightarrow{MB}\right|\) nhỏ nhất khi và chỉ khi M là hình chiếu của I trên \(\Delta\)
Gọi \(\left(x;y\right)\) là tọa độ hình chiếu của I trên \(\Delta\). Khi đó ta có hệ phương trình :
\(\begin{cases}x+y+1=0\\\frac{x+1}{1}=\frac{y-2}{1}\end{cases}\) \(\Leftrightarrow\begin{cases}x+y+1=0\\x-y+3=0\end{cases}\)
Giải hệ thu được \(x=-2;y=1\) Vạy điểm \(M\in\Delta\) mà \(\left|\overrightarrow{MA}+\overrightarrow{MB}\right|\) nhỏ nhất là \(M\equiv I\left(-2;1\right)\)
b) gọi J là điểm thỏa mãn \(2\overrightarrow{JA}+3\overrightarrow{JB}\)=0 khi đó \(J\left(-\frac{8}{5};\frac{9}{5}\right)\) và với mọi điểm M của mặt phẳng đều có
\(2MA^2+3MB^2=2JA^2+3JB^2+5MJ^2\)
suy ra \(M\in\Delta\)mà \(2MA^2+3MB^2\)nhỏ nhất khi và chỉ khi M là hình chiếu của J trên\(\Delta\)
Gọi (x;y) là tọa độ hình chiếu của J trên \(\Delta\).khi đó ta có phương trình
\(\begin{cases}x+y+1=0\\x+\frac{8}{5}=y-\frac{9}{5}\end{cases}\)\(\Leftrightarrow\begin{cases}x+y+1=0\\x-y-\frac{17}{5}=0\end{cases}\)
Giải hệ thu được : \(x=\frac{5}{6};y=-\frac{11}{5}\)
Vậy điểm M cần tìm là : \(M\left(\frac{6}{5};\frac{-11}{5}\right)\)

+câu a:+ gọi d là đường thẳng qua O vuông góc với \(\Delta\): pt d :x+y+m=0 , O(00) \(\in d\Rightarrow m=0\). vậy pt d :x+y =0
+giao điểm H của d và \(\Delta\) thỏa \(\left\{{}\begin{matrix}x-y+2=0\\x+y=0\end{matrix}\right.\Rightarrow H\left(-1;1\right)\)
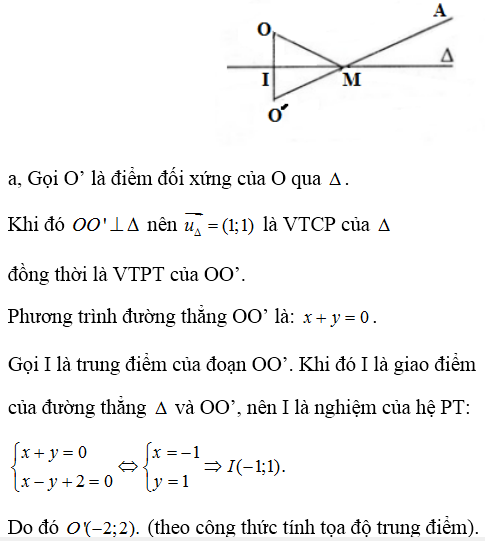
+goi O' la diem doi xung voi O qua d \(\Rightarrow\)H là trung điểm OO'
\(\Rightarrow O'\left(-2;2\right)\)
câu b : goi M (a;b) \(\in\Delta\Rightarrow M\left(a;a+2\right)\)
+ O' doi xung O qua \(\Delta\) nen MO = MO'.
+ OM+MA=O'M+MA\(\ge OA\) dấu bằng xảy ra khi O',M,A thang hang \(\Leftrightarrow\overrightarrow{O'M}\)cùng phương với \(\overrightarrow{O'A}\)
+ \(\overrightarrow{O'M}=\left(a+2;a\right);\overrightarrow{O'A}=\left(4;-2\right)\)
\(\Rightarrow\dfrac{a+2}{4}=\dfrac{a}{-2}\Rightarrow a=\dfrac{-2}{3}\Rightarrow M\left(\dfrac{-2}{3};\dfrac{4}{3}\right)\)

M \(\varepsilon\Delta\)=> M ( 1+ t; 2 + t)
MA2 = (t + 2)2 + t2 = 2 t2 + 4t + 4
MB2 = (t - 2)2 + (t + 1)2 = 2t2 - 2t + 5
MA2 +MB2 = 2t2 + 4t + 4 + 2t2 - 2t + 5 = 4t2 + 2t + 9 = 4t2 + 2.2t.1/2 + 1/4 + 35/4
= ( 2t + 1/2 )2 + 35/4 >= 35/4
vậy min của MA2 + MB2 = 35/4 <=> t = -1/4 => M (3/4 ; 7/4)
#mã mã#

Phương trình tổng quát \(\Delta\):
\(\dfrac{x-2}{2}=\dfrac{y-3}{1}\)=> x-2y+4=0
a. Vì M \(\in\) \(\Delta\)=> M (2y-4;y)
Theo giả thiết, MA=5 <=> \(\sqrt{(-2y+4)^{2}+(1-y)^{2}}\)=5
<=> \(5y^2-18y-8=0\)
<=>y=4 và y=\(\dfrac{-2}{5}\)
Vậy M1(4;4) và M2(\(\dfrac{-24}{5};\dfrac{-2}{5}\))
b. Gọi I là tọa độ giao điểm của đường thẳng \(\Delta\)với đường thẳng (d): x+y+1=0
Ta có hệ phương trình:
\(\begin{cases} x-2y+4=0\\ x+y+1=0 \end{cases}\)
\(\begin{cases} x=-2\\ y=1 \end{cases}\)
=> I(-2;1) là giao điểm của đường thẳng \(\Delta\)với đường thẳng d
c. Nhận thấy, điểm A\(\notin\)\(\Delta\)
Để AM ngắn nhất <=> M là hình chiếu của A trên đường thẳng \(\Delta\)
Vì M\(\in\Delta\)=> M(2y-4;y)
Ta có: Vectơ chỉ phương của \(\overrightarrow{AM}\)là \(\overrightarrow{u}\)(2;1)
\(\overrightarrow{AM}\) (2y-4;y-1)
Vì A là hình chiếu của A trên \(\Delta\)nên \(\overrightarrow{AM}\)\(\perp\Delta\)
<=> \(\overrightarrow{AM}\)\(\perp\overrightarrow{u}\)
<=> \(\begin{matrix}\overrightarrow{AM}&\overrightarrow{u}\end{matrix}\) =0
<=> 2(2y-4)+(y-1)=0
<=> 5y-9=0
<=> y= \(\dfrac{9}{5}\)
=> B (\(\dfrac{-2}{5}\);\(\dfrac{4}{5}\))

a. Vì \(2-2.5+3=-5< 0\) và \(-4-2.5+3=-11< 0\) nên A, B cùng phía với đường thẳng \(\Delta\).
Gọi \(A'\left(x;y\right)\) là điểm đối xứng với A qua \(\Delta\), khi đó (x;y) là nghiệm của hệ :
\(\begin{cases}\frac{x-2}{1}=\frac{y-5}{-2}\\\frac{x-2}{1}-2.\frac{y+5}{2}+3=0\end{cases}\)
Giải hệ ta được : \(\left(x;y\right)=\left(4;1\right)\) suy ra \(\overrightarrow{A'B}=\left(-8;4\right)=4\left(-2;1\right)\)
Do đó đường thẳng A'B có phương trình tham số \(\begin{cases}x=4-2t\\y=1+t\end{cases}\)\(;t\in R\)
Suy ra điểm C cần tìm có tọa độ là nghiệm của hệ :
\(\begin{cases}x=4-2t\\y=1+t\\x-2y+3=0\end{cases}\)
Giải hệ ta có điểm C \(\left(\frac{3}{2};\frac{9}{4}\right)\)
b. Gọi I là trung điểm của AB. Khi đó\(I\left(-1;5\right)\) và \(\overrightarrow{CA}+\overrightarrow{CB}=2\overrightarrow{CI}\), với mọi C.
Vậy \(C\in\Delta\) : \(\left|\overrightarrow{CA}+\overrightarrow{CB}\right|\) bé nhất \(\Leftrightarrow\left|CI\right|\) bé nhất \(\Leftrightarrow C\) là hình chiếu của I trên \(\Delta\)
Nếu \(C\left(x;y\right)\) là hình chiếu của I trên \(\Delta\) thì (x;y) là nghiệm của hệ :
\(\begin{cases}\frac{x+1}{1}=\frac{y-5}{-2}\\x-2y+3=0\end{cases}\)
Giải hệ thu được : \(\left(x;y\right)=\left(\frac{3}{5};\frac{9}{5}\right)\) vậy \(C\left(\frac{3}{5};\frac{9}{5}\right)\)
Đường thẳng \(\Delta\) có vecto pháp tuyến \(\overrightarrow{n}=\left(1;-2\right)\) nên nhận \(\overrightarrow{u}=\left(2;1\right)\) làm vecto chỉ phương.
Từ đó để ý rằng đường thẳng \(\Delta\) cắt Ox tại \(M\left(-3;0\right)\) nên \(\Delta\) có phương trình dạng tham số :
\(\begin{cases}x=-3+2t\\y=t\end{cases}\) \(\left(t\in R\right)\)
a. Xét \(C\left(-3+2t;t\right)\in\Delta\), khi đó :
\(CA+CB=\sqrt{\left(5-2t\right)^2+\left(5-t\right)^2}+\sqrt{\left(2t+1\right)^2+\left(t-5\right)^2}\)
\(=\sqrt{5t^2-30t+50}+\sqrt{5t^2-6t+26}\)
\(=\sqrt{\left(\sqrt{5}t-3\sqrt{5}\right)^2}+\sqrt{\left(\frac{3}{\sqrt{5}}-\sqrt{5}t\right)^2+\frac{121}{5}}\)
\(\ge\sqrt{\left(\frac{3}{\sqrt{5}}-3\sqrt{5}\right)^2+\left(\sqrt{5}+\frac{11}{\sqrt{5}}\right)^2}=4\sqrt{5}\)
Dấu đẳng thức xảy ra khi và chỉ khi
\(\frac{\sqrt{5}t-3\sqrt{5}}{\frac{3}{\sqrt{5}}-\sqrt{5}t}=\frac{5}{11}\Leftrightarrow t=\frac{9}{4}\)
Từ đó tìm được : \(C\left(\frac{3}{2};\frac{9}{4}\right)\)
b. Với \(C\left(=3+2t;t\right)\in\Delta\) ta có \(\overrightarrow{CA}=\left(5-2t;5-t\right)\) và \(\overrightarrow{CB}=\left(-1-2t;5-t\right)\)
Suy ra : \(\overrightarrow{CA}+\overrightarrow{CB}=\left(4-4t;10-2t\right)\) và do đó :
\(\left|\overrightarrow{CA}+\overrightarrow{CB}\right|=\sqrt{\left(4-4t\right)^2+\left(10-2t\right)^2}=\sqrt{\left(2\sqrt{5}t-\frac{18}{\sqrt{5}}\right)^2+\frac{256}{5}}\ge\frac{16}{\sqrt{5}}\)
Dấu đẳng thức xảy ra khi và chỉ khi \(t=\frac{9}{5}\)
Do đó điểm C cần tìm là \(\left(\frac{3}{5};\frac{9}{5}\right)\)


Ta nhận thấy A và B nằm cùng phía với Δ
a. M ∈ Δ => M(m ; -1 - 2m)
=> \(\overrightarrow{MA}\) = ( -m ; 4 + 2m) ; \(\overrightarrow{AB}\) = (1 ; 2)
Ta có : \(\left|MA-MB\right|\le AB\)
Dấu "=" xảy ra ⇔ A, M, B thẳng hàng
⇔ -m = \(\frac{4+2m}{2}\) ⇔ m = -1 => M ( -1 ; 1)
b. N ∈ Δ => N(n ; -1 - 2n)
Qua Δ lấy B' đối xứng với B => B' (\(\frac{-27}{5};\frac{9}{5}\))
=> \(\overrightarrow{B'A}\) = (\(\frac{27}{5};\frac{6}{5}\)) ; \(\overrightarrow{AN}\) = (n ; - 4 - 2n)
Mặt khác: NA + NB = NA + NB' ≥ AB'
Dấu "=" xảy ra ⇔ N, A, B' thẳng hàng
⇔ \(\frac{\frac{27}{5}}{n}=\frac{\frac{6}{5}}{-4-2n}\) ⇔ n = \(\frac{-9}{5}\) => N(\(\frac{-9}{5};\frac{13}{5}\))