Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
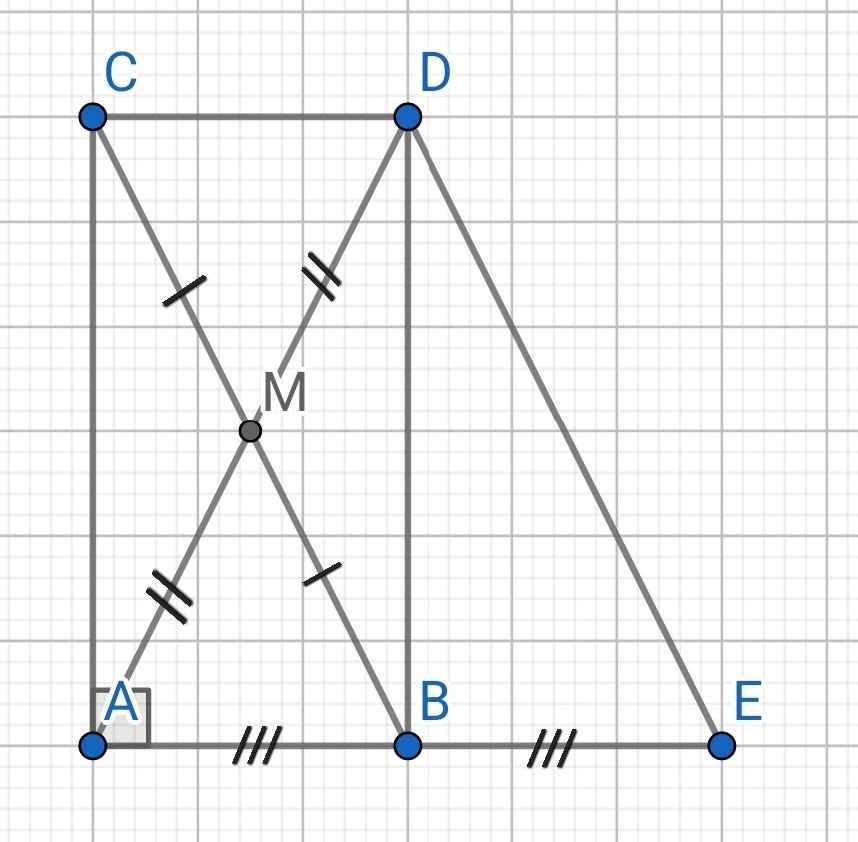a) Tứ giác ABDC có:
M là trung điểm của BC (gt)
M là trung điểm của AD (gt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (∆ABC vuông tại A)
⇒ ABDC là hình chữ nhật
b) Do ABDC là hình chữ nhật (cmt)
⇒ CD = AB (1)
Do B là trung điểm của AE (gt)
⇒ BE = AB = AE : 2 (2)
Từ (1) và (2) ⇒ CD = BE
Do ABDC là hình chữ nhật (cmt)
⇒ CD // AB
⇒ CD // BE
Tứ giác BEDC có:
CD // BE (cmt)
CD = BE (cmt)
⇒ BEDC là hình bình hành
c) Do ABDC là hình chữ nhật (cmt)
⇒ AC // BD
Do đó AC, BD, EK đồng quy là vô lý
Em xem lại đề nhé!
bạn tự vẽ hình nha
a)Trong tam giác ABC có: E là trung điểm của AB; D là trung điểm của AC
=> ED là đường trung bình của ABC
=> ED//BC và ED=\(\frac{1}{2}\)BC (1)
=> tứ giác BEDC là hình thang
b) Trong tam giác CBG có: M là trung điểm của GB; N là trung điểm của GC
=> MN là đường trung bình của tam giác CBG
=> MN//BC và MN=\(\frac{1}{2}\)BC (2)
Từ (1) và (2) => ED//MN và ED = MN
=> tứ giác MEDN là hình bình hành
c) Tứ giác MEDN là hcn <=> MEDN là hbh
Có 2 đường chéo bằng nhau <=> EN = DM
Mà EN = \(\frac{2}{3}\)EC; DM = \(\frac{2}{3}\)DB
Lại có: hình thang BEDC có EC = BD
=> BEDC là hình thang cân tại A
Vậy tam giác ABC tại thì tứ giác MEDN là hcn
hình tự vẽ nha bạn
a) tam giác ABC có E là tđ của AB,D là tđ của AC
=> ED là đtb của tam giác ABC
=> ED// BC và ED=1/2BC (1)
=> tứ giác BEDC là hình thang
b) tam giác GBC có M là tđ của GB,N là tđcủa GC
=> MN là đtb của tam giác GBC
=> MN//BC và MN=1/2BC (2)
từ (1),(2)=> ED//MN và ED=MN
=> tứ giác MEDN là hbh
c) tứ giác MEDN là hcn <=> MEDN là hbh có 2 đường chéo bằng nhau
<=> EN=DM
mà EN=2/3EC,DM=2/3DB=> EC=BD
hình thang BEDC có EC=BD=> BEDC là h thang cân => góc EBC=DCB
=> tam giác ABC cân tại A
vậy tam giác ABC cân tại A thì ......
d) kẻ đường cao AH
gọi O là gđ của AH và ED
tam giác AHB có E là tđ của AB,EO//BH (ED//BC)
=> O là tđ của AH
=> OH=1/2AH
Sbedc=1/2(ED+BC).OH
=1/2.(1/2BC+BC).1/2AH
=1/2.3/2BC.1/2AH
=3/4BC.1/2AH
=3/8BC.AH
=1/2.AH.BC.3/4
=3/4 Sabc
a: Xét ΔAED và ΔACB có
\(\dfrac{AE}{AC}=\dfrac{AD}{AB}\)
\(\widehat{EAD}=\widehat{CAB}\)
Do đó: ΔAED\(\sim\)ΔACB
Suy ra: \(\widehat{AED}=\widehat{ACB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên DE//BC
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
mà EC=BD
nên BEDC là hình thang cân