Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có \(\Delta'=\left(m+4\right)^2-m^2+8=m^2+8m+16-m^2+8=24>0\)
Nên pt có nghiệm với mọi m
Theo hệ thức Vi-ét \(\hept{\begin{cases}x_1+x_2=2\left(m+4\right)\\x_1x_2=m^2-8\end{cases}}\)
a,(Phải là GTLN nhá)
Có \(x_1+x_2-3x_1x_2=2\left(m+4\right)-3\left(m^2-8\right)\)
\(=2m+8-3m^2+24\)
\(=-3m^2+2m+32\)
\(=-3\left(m^2-\frac{2}{3}m+\frac{1}{9}\right)+\frac{95}{3}\)
\(=-3\left(m-\frac{1}{3}\right)^2+\frac{95}{3}\le\frac{95}{3}\)
Dấu "=" <=> m = 1/3
b, Thấy tổng x_1 ; x_2 là bậc 1 của m , tích là bậc 2 của m nên ko tồn tại hệ thức thỏa mãn đề

- \(\Delta^'=m^2-\left(m-1\right)\left(m+1\right)=m^2-m^2+1=1>0\)vậy phương trình luôn có hai nghiệm với mọi \(m\ne1\)
- Theo viet ta có : \(\hept{\begin{cases}x_1+x_2=2m\\x_1x_2=m+1\end{cases}}\)\(\Rightarrow m+1=5\Rightarrow m=4\Rightarrow x_1+x_2=2m=2.4=8\)
- từ hệ thức viet ta khử m được hệ thức liên hệ giữa 2 nghiệm ko phụ thuộc m: thấy \(x_1+x_2-2x_2x_1=2m-2\left(m+1\right)=-2\)
- \(\frac{x_1}{x_2}+\frac{x_2}{x_1}=-\frac{5}{2}\Leftrightarrow\frac{x_1^2+x_2^2}{x_1x_2}=-\frac{5}{2}\Leftrightarrow\frac{\left(x_1+x_2\right)^2-2x_1x_2}{x_1x_2}=-\frac{5}{2}\)\(\Leftrightarrow\frac{4m^2-2m-2}{m+1}=-\frac{5}{2}\Rightarrow8m^2-4m-4=-5m-5\left(m\ne-1\right)\)\(\Leftrightarrow8m^2+m+1=0\left(vn\right)\)không có giá trị nào của m thỏa mãn

\(\Delta'=\left[-\left(m+4\right)\right]^2-1\left(m^2-8\right)=m^2+8m+16-m^2+8=8m+24\)
Để pt có 2 nghiệm thì \(\Delta'\ge0\Leftrightarrow8m+24\ge0\Leftrightarrow m\ge-3\)
Áp dụng định lý Vi-ét ta có:\(\left\{{}\begin{matrix}x_1+x_2=2m+8\\x_1x_2=m^2-8\end{matrix}\right.\)
\(A=x^2_1+x^2_2-x_1-x_2\\ =\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)\\ =\left(2m+8\right)^2-2\left(m^2-8\right)-\left(2m+8\right)\\ =4m^2+32m+64-2m^2+16-2m-16\\ =2m^2+30m+64\)
Amin=\(-\dfrac{97}{2}\)\(\Leftrightarrow m=-\dfrac{15}{2}\)
\(B=x^2_1+x^2_2-x_1x_2\\ =\left(x_1+x_2\right)^2-3x_1x_2\\ =\left(2m+8\right)^2-3\left(m^2-8\right)\\ =4m^2+32m+64-3m^2+24\\ =m^2+32m+88\)
Bmin=-168\(\Leftrightarrow\)m=-16

\(x^2-2\left(m+1\right)x+3\left(m+1\right)-3=0\)
\(x^2-2nx+3n+3=\left(x-n\right)^2-\left(n^2-3n+3\right)=0\)\(\left(x-n\right)^2=\left(n-\frac{3}{2}\right)^2+\frac{3}{4}=\frac{\left(2n-3\right)^2+3}{4}>0\forall n\) vậy luôn tồn tại hai nghiệm
\(\orbr{\begin{cases}x_1=\frac{n-\sqrt{\left(2n-3\right)^2+3}}{2}\\x_2=\frac{n+\sqrt{\left(2n-3\right)^2+3}}{2}\end{cases}}\)
a) \(\frac{x_1}{x_2}=\frac{4x_1-x_2}{x_1}\Leftrightarrow\frac{x_1^2-4x_1x_2+x_2^2}{x_1x_2}=0\)
\(x_1x_2=n^2-\frac{\left(2n-3\right)^2+3}{4}=\frac{4n^2-4n^2+12n-9-3}{4}=3n-3\)
với n=1 hay m=0 : Biểu thức cần C/m không tồn tại => xem lại đề

Theo Vi et : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=2m+2\\x_1x_2=\frac{c}{a}=m^2+3\end{cases}}\)
\(A=m^2+3+2m+2=m^2+2m+5=\left(m+1\right)^2+4\ge4\)
Dấu ''='' xảy ra khi m = -1
Vậy GTNN A là 4 khi m =-1

Pt có nghiệm khi \(\Delta\ge0\)
\(\Leftrightarrow\left(m-1\right)^2-4\left(5m-5\right)\ge0\)
\(\Leftrightarrow m^2-2m+1-20m+20\ge0\)
\(\Leftrightarrow m^2-22m+21\ge0\)
\(\Leftrightarrow\orbr{\begin{cases}m\le1\\m\ge21\end{cases}}\)
Theo hệ thức Vi-ét \(\hept{\begin{cases}x_1+x_2=1-m\\x_1x_2=5m-5\end{cases}}\)
Chắc đề là \(x_1^2+x_2^2=3x_1x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2=5x_1x_2\)
\(\Leftrightarrow\left(1-m\right)^2=5.\left(5m-5\right)\)
\(\Leftrightarrow1-2m+m^2=25m-25\)
\(\Leftrightarrow m^2-27m+26=0\)
\(\Leftrightarrow\orbr{\begin{cases}m=26\\m=1\end{cases}\left(Tm\right)}\)
Vậy .........

\(\Delta'=\left(m+1\right)^2-\left(2m-3\right)=m^2+4>0,\forall m\inℝ\)
nên phương trình luôn có hai nghiệm phân biệt \(x_1+x_2\).
Theo định lí Viete:
\(\hept{\begin{cases}x_1+x_2=2m+2\\x_1x_2=2m-3\end{cases}}\)
\(P=\left|\frac{x_1+x_2}{x_1-x_2}\right|=\frac{\left|x_1+x_2\right|}{\left|x_1-x_2\right|}=\frac{\left|x_1+x_2\right|}{\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}}\)
\(=\frac{\left|2m+2\right|}{\sqrt{\left(2m+2\right)^2-4\left(2m-3\right)}}=\frac{\left|2m+2\right|}{\sqrt{4m^2+16}}=\frac{\left|m+1\right|}{\sqrt{m^2+4}}\ge0\)
Dấu \(=\)xảy ra khi \(m=-1\).

a) Nếu m = -1 thì : \(4x-3=0\Leftrightarrow x=\frac{3}{4}\) => pt có một nghiệm
Nếu \(m\ne-1\) , xét \(\Delta'=\left(m-1\right)^2-\left(m+1\right)\left(m-2\right)=m^2-2m+1-\left(m^2-m-2\right)=-m+3\)
Để pt có hai nghiệm phân biệt thì \(\Delta>0\) , tức là \(3-m>0\Leftrightarrow m< 3\)
Vậy để pt có hai nghiệm phân biệt thì \(\begin{cases}m< 3\\m\ne-1\end{cases}\)
b) Thay x = 2 vào pt đã cho , tìm được m = -6
Suy ra pt : \(-5x^2+14x-8=0\Leftrightarrow\left(5x-4\right)\left(x-2\right)=0\) \(\Leftrightarrow\left[\begin{array}{nghiempt}x=2\\x=\frac{4}{5}\end{array}\right.\)
Vậy nghiệm còn lại là x = 4/5
c) Áp dụng hệ thức Vi-et , ta có : \(\begin{cases}x_1+x_2=2\left(m-1\right)\\x_1.x_2=m-2\end{cases}\)
\(\frac{1}{x_1}+\frac{1}{x_2}=\frac{7}{4}\Leftrightarrow4\left(x_1+x_2\right)=7x_1.x_2\)
\(\Rightarrow4.\left(2m-2\right)=7.\left(m-2\right)\Leftrightarrow8m-8=7m-14\Leftrightarrow m=-6\)
d) Ta có : \(A=2\left(x_1^2+x_2^2\right)+x_1.x_2=2\left(x_1+x_2\right)^2-3x_1.x_2=8\left(m-1\right)^2-3\left(m-2\right)\)
\(=8m^2-19m+14=8\left(m-\frac{19}{16}\right)^2+\frac{87}{32}\ge\frac{87}{32}\)
=> Min A = 87/32 <=> m = 19/16
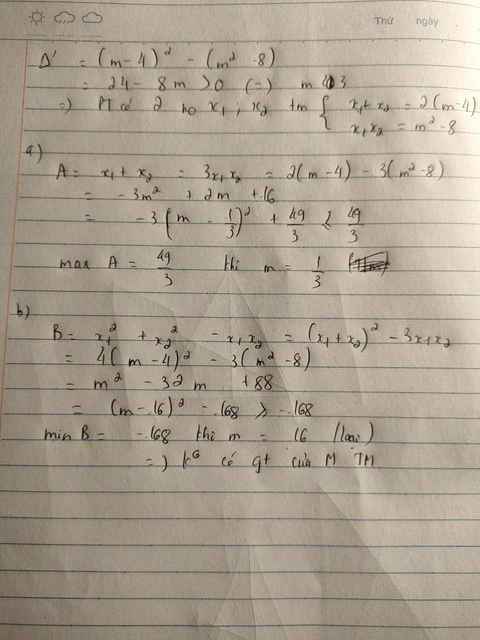
\(\Delta'=\left(m+4\right)^2-\left(m^2-8\right)=8m+24\ge0\Rightarrow m\ge-3\)
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+4\right)\\x_1x_2=m^2-8\end{matrix}\right.\)
a/ \(A=x_1^2+x_2^2-3x_1x_2=\left(x_1+x_2\right)^2-5x_1x_2\)
\(=4\left(m+4\right)^2-5\left(m^2-8\right)\)
\(=-m^2+32m+104=360-\left(m-16\right)^2\le360\)
\(A_{max}=360\) khi \(m=16\)
\(B=\left(x_1+x_2\right)^2-3x_1x_2\)
\(=4\left(m+4\right)^2-3\left(m^2-8\right)\)
\(=m^2+32m+88=\left(m+3\right)\left(m+29\right)+1\ge1\)
\(\Rightarrow B_{min}=1\) khi \(m=-3\)
b/ Từ Viet: \(\left\{{}\begin{matrix}\frac{x_1+x_2-8}{2}=m\\x_1x_2+8=m^2\end{matrix}\right.\)
\(\Rightarrow\left(\frac{x_1+x_2-8}{2}\right)^2=x_1x_2+8\)
Đây là hệ thức liên hệ 2 nghiệm ko phụ thuộc m (bạn có thể rút gọn thêm)