NN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
2
14 tháng 5 2017
Hoành độ giao điểm của hai đồ thị thỏa mãn pt : \(x^2=-x+2\Leftrightarrow x^2+x-2=0\)
Giải ra ta được x1 , x2 .Thay x1 ,x2 vừa tìm được vào một trong hai công thức hàm số,ta được y1,y2.
2 tháng 3 2022
Phương trình hoành độ giao điểm là:
\(x^2-x\sqrt{3}+\sqrt{3}-1=0\)
\(\text{Δ}=\left(\sqrt{3}\right)^2-4\cdot1\cdot\left(\sqrt{3}-1\right)=3-4\sqrt{3}+4=7-4\sqrt{3}=\left(2-\sqrt{3}\right)^2\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{\sqrt{3}-2+\sqrt{3}}{2}=\sqrt{3}-1\\x_2=\dfrac{\sqrt{3}+2-\sqrt{3}}{2}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y_1=4-2\sqrt{3}\\y_2=1\end{matrix}\right.\)
30 tháng 4 2023
PTHĐGĐ là:
1/2x^2+x-m=0
Δ=1^2-4*1/2*(-m)=1+2m
Để (d) tiếp xúc (P) thì 2m+1=0
=>m=-1/2
=>1/2x^2+x+1/2=0
=>x^2+2x+1=0
=>x=-1
=>y=1/2*(-1)^2=1/2
30 tháng 4 2023
a,
Xét pt hoành độ giao điểm của (P) và (d): \(x^2+2x-2m=0\) (1)
\(\Delta=2^2-4\left(-2m\right)=4+8m\)
Để (d) tiếp xúc (P) thì pt (1) có nghiệm kép \(\Rightarrow\Delta=4+8m=0\)
\(\Rightarrow m=-\dfrac{1}{2}\)
Thay \(m=-\dfrac{1}{2}\) vào (1) \(\Rightarrow x^2+2x+1=0\)
\(\Rightarrow\left(x+1\right)^2=0\) \(\Rightarrow x=-1\)
\(\Rightarrow y=\dfrac{1}{2}\left(-1\right)^2=\dfrac{1}{2}\)
Vậy (d) tiếp xúc (P) khi \(m=-\dfrac{1}{2}\) tại tọa độ \(\left(-1;\dfrac{1}{2}\right)\).
CM
10 tháng 1 2019
1) Xác định được ít nhất hai điểm phân biệt thuộc đường thẳng d. Chẳng hạn: A ( − 3 ; 0 ) ; B ( 0 ; 3 ) .
Xác định được đỉnh và ít nhất hai điểm thuộc (P) . Chẳng hạn : O ( 0 ; 0 ) ; C ( 6 ; 9 ) ; E ( − 6 ; 9 ) .
Đồ thị
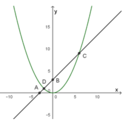
2) Phương trình hoành độ giao điểm: 1 4 x 2 = x + 3 ⇔ 1 4 x 2 − x − 3 = 0 ⇔ x = − 2 hoặc x= 6
Tọa độ giao điểm là D ( − 2 ; 1 ) v à C ( 6 ; 9 ) .
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2023
Phương trình hoành độ giao điểm (d) và (P):
\(x^2=2x-m\Leftrightarrow x^2-2x+m=0\) (1)
(d) tiếp xúc (P) khi và chỉ khi (1) có nghiệm kép
\(\Leftrightarrow\Delta'=1-m=0\)
\(\Rightarrow m=1\)
9 tháng 5 2023
a: Thay x=2 vào (P),ta được:
y=2^2/2=2
2: Thay x=2 và y=2 vào (d), ta được:
m-1+2=2
=>m-1=0
=>m=1
Đề bài yêu cầu gì?