Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

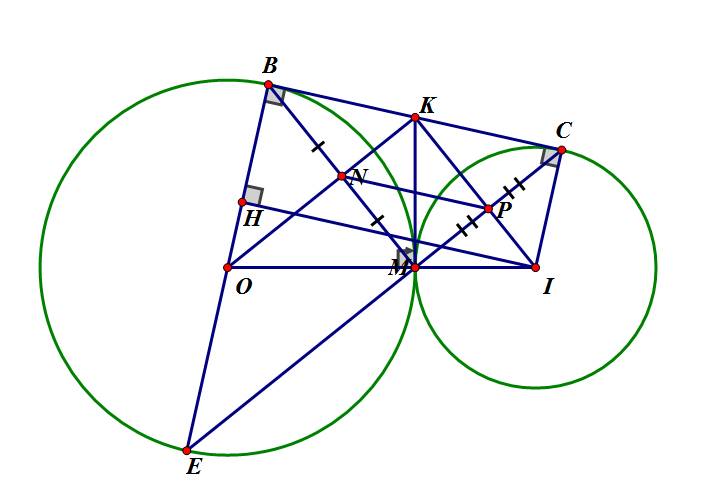
a) Trong (O) có: KB,KM là hai tiếp tuyến cắt nhau tại K.
\(\Rightarrow KB=KM\left(1\right)\).
Trong (I) có: KC,KM là hai tiếp tuyến cắt nhau tại K.
\(\Rightarrow KC=KM\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow KB=KC\)
△BME nội tiếp đường tròn (O) đường kính BE.
⇒△BME vuông tại MM.
\(\Rightarrow\widehat{BME}=90^0\)
b) Ta có: K thuộc đường trung trực của BM (\(KB=KM\))
O thuộc đường trung trực của BM \(\left(OB=OM\right)\)
⇒OK là đường trung trực của BM mà OK cắt BM tại N.
⇒N là trung điểm BM.
- Ta có: K thuộc đường trung trực của CM (\(KC=KM\))
I thuộc đường trung trực của CM \(\left(IC=IM\right)\)
⇒IK là đường trung trực của CM mà IK cắt CM tại P.
⇒P là trung điểm IK và \(CM\perp IK\) tại P.
Xét △BCM có: N là trung điểm BM, P là trung điểm CM.
⇒NP là đường trung bình của △BCM.
⇒NP//CM.
c) *Hạ \(IH\perp OB\) tại H.
Xét tứ giác BCIH có: \(\widehat{HBC}=\widehat{BCI}=\widehat{BHI}=90^0\)
⇒BCIH là hình chữ nhật.
\(\Rightarrow BC=IH;IC=BH=r\)
Xét △ICK vuông tại C có IP là đường cao:
\(\Rightarrow IK.IP=IC^2=r^2\)
Xét △OHI vuông tại H có:
\(HI^2+OH^2=OI^2\)
\(\Rightarrow HI=\sqrt{OI^2-OH^2}=\sqrt{\left(r+R\right)^2-\left(r-R\right)^2}=\sqrt{4Rr}=2\sqrt{Rr}\)
Mà \(BC=HI\Rightarrow BC=2\sqrt{Rr}\left(1'\right)\)
Ta có: \(2\sqrt{IM.IO-IK.IP}=2\sqrt{r\left(r+R\right)-r^2}=2\sqrt{Rr}\left(2'\right)\)
\(\left(1'\right),\left(2'\right)\Rightarrow BC=2\sqrt{IM.IO-IK.IP}\)

a: Xét (O) có
MB,MA là các tiếp tuyến
Do đó: MB=MA
Xét (O') có
MA,MC là các tiếp tuyến
Do đó: MA=MC
Ta có: MB=MA
MA=MC
Do đó:MB=MC
=>M là trung điểm của BC
Xét ΔABC có
AM là đường trung tuyến
\(AM=\dfrac{BC}{2}\left(=BM\right)\)
Do đó: ΔABC vuông tại A
b: ta có: MB=MA
=>M nằm trên đường trung trực của AB(1)
Ta có: OB=OA
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại E
ta có: MA=MC
=>M nằm trên đường trung trực của AC(3)
ta có: O'A=O'C
=>O' nằm trên đường trung trực của AC(4)
từ (3) và (4) suy ra MO' là trung trực của AC
=>MO'\(\perp\)AC tại F
Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
=>AEMF là hình chữ nhật

a) Theo tính chất hai tiếp tuyến cắt nhau ta có IA = IB = IC.
Do đó tam giác ABC vuông tại A.
Lại có \(IO_1\perp AB;IO_2\perp AC\) nên tam giác \(IO_1O_2\) vuông tại I.
b) Đầu tiên ta chứng minh kết quả sau: Cho hai đường tròn (D; R), (E; r) tiếp xúc với nhau tại A. Tiếp tuyến chung BC (B thuộc (D), C thuộc (E)). Khi đó \(BC=2\sqrt{Rr}\).
Thật vậy, kẻ EH vuông góc với BD tại H. Ta có \(DH=\left|R-r\right|;DE=R+r\) nên \(BC=EH=\sqrt{DE^2-DH^2}=2\sqrt{Rr}\).
Trở lại bài toán: Giả sử (O; R) tiếp xúc với BC tại M.
Theo kết quả trên ta có \(BM=2\sqrt{R_1R};CM=2\sqrt{RR_2};BC=2\sqrt{R_1R_2}\).
Do \(BM+CM=BC\Rightarrow\sqrt{R_1R}+\sqrt{R_2R}=\sqrt{R_1R_2}\Rightarrow\dfrac{1}{\sqrt{R}}=\dfrac{1}{\sqrt{R_1}}+\dfrac{1}{\sqrt{R_2}}\).
P/s: Hình như bạn nhầm đề

a) MA,MB là các tiếp tuyến của đường tròn (O) (gt).
Theo tính chất của hai tiếp tuyến cắt nhau, ta có MA=MB, MO là tia phân giác AMBˆ
ΔMAB cân tại M(MA=MB)
Có MO là đường phân giác nên đồng thời là đường cao
=>MO┴AB=>MEAˆ=900
Chứng minh tương tự có MO’ là tia phân giác góc AMCˆ và MFAˆ=900
MO,MO′ là tia phân giác của hai góc kẻ bù AMBˆ,AMCˆ⇒EMFˆ=900
Tứ giác AEMF là hình chữ nhật (vì EMFˆ=MEAˆ=MFAˆ=900
b) ΔMAO vuông tại A có AE là đường cao nên ME.MO=MA2
Tương tự, ta có: MF.MO′=MA2
Do đó, ME.MO=MF.MO′(=MA2)