Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
AM,AC là tiếp tuyến
Do đó: AM=AC và OA là tia phân giác của \(\widehat{MOC}\)
=>\(\widehat{MOC}=2\cdot\widehat{MOA}\)
Xét (O) có
BM,BD là tiếp tuyến
Do đó: BM=BD và OB là phân giác của \(\widehat{MOD}\)
=>\(\widehat{MOD}=2\cdot\widehat{MOB}\)
\(\widehat{MOC}+\widehat{MOD}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{MOA}+2\cdot\widehat{MOB}=180^0\)
=>\(2\left(\widehat{MOA}+\widehat{MOB}\right)=180^0\)
=>\(\widehat{MOA}+\widehat{MOB}=\dfrac{180^0}{2}=90^0\)
=>\(\widehat{AOB}=90^0\)
b: AB=AM+BM
mà AM=AC và BM=BD
nên AB=AC+BD
c: Xét ΔOAB vuông tại O có OM là đường cao
nên \(AM\cdot MB=OM^2\)
=>\(AC\cdot BD=R^2\) không đổi khi M di chuyển trên (O)

Cô hướng dẫn nhé nguyen van vu :)
K
a. Ta có góc COD = COM + MOD = \(\frac{AOM}{2}+\frac{BOM}{2}=\frac{180}{2}=90^o\)
b. Dễ thấy E là trung điểm CD, O là trung điểm AB nên OE song song AC. Vậy OE vuông góc AB.
c. Gọi MH là đường thẳng vuông góc AB, Ta chứng minh BC, AD đều cắt MH tại trung điểm của nó.
Gọi I là giao của AM và BD. Đầu tiên chứng minh ID = DB. Thật vậy, góc MID=IMD (Cùng bằng cung AM/2)
nên ID =MD, mà MD=DB nên ID=DB.
Gọi K là giao của MH và AD.
Theo Talet , \(\frac{MK}{DI}=\frac{AK}{AD}=\frac{KH}{BD}\Rightarrow MK=KH\)
Tương tự giao điểm của BC với MH cũng là trung điểm MH.
Tóm lại N trùng K hay MN vuông góc AB.

a: góc OAC+góc OMC=180 độ
=>OACM nội tiếp
b: góc BOM=2*60=120 độ
=>góc BDM=60 độ
=>ΔBMD đều
\(S_{qMB}=\dfrac{pi\cdot R^2\cdot120}{360}=\dfrac{1}{3}\cdot pi\cdot R^2\)

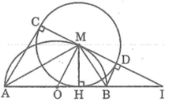
Trong đường tròn (M; MH), theo tính chất hai tiếp tuyến cắt nhau, ta có:
- MA là tia phân giác của góc HMC

Vậy C, M, D thẳng hàng.