Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

d/ Ta có:
\(A=\left(-x+\sqrt{x}-\dfrac{1}{4}\right)+\dfrac{1}{4}\)
\(=\dfrac{1}{4}-\left(\sqrt{x}-\dfrac{1}{2}\right)^2\le\dfrac{1}{4}\)
Vậy GTLN là \(A=\dfrac{1}{4}\) đạt được tại \(x=\dfrac{1}{4}\)
b/ \(\sqrt{1x}-x\)
c/ Ta có:
x < 1
\(\Rightarrow\sqrt{x}< 1\)
\(\Rightarrow1-\sqrt{x}>0\)
Ta lại có: x > 0
\(\Rightarrow A=\sqrt{x}-x=\sqrt{x}\left(1-\sqrt{x}\right)>0\)

a) ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)
Ta có: \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right)\cdot\left(\dfrac{1}{1+\sqrt{x}}+\dfrac{2}{x-1}\right)\)
\(=\left(\dfrac{x}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right)\cdot\left(\dfrac{\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}-1+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
b) Để P>0 thì \(\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}>0\)
mà \(\sqrt{x}+1>0\forall x\) thỏa mãn ĐKXĐ
nên \(\sqrt{x}\left(\sqrt{x}-1\right)>0\)
mà \(\sqrt{x}>0\forall x\) thỏa mãn ĐKXĐ
nên \(\sqrt{x}-1>0\)
\(\Leftrightarrow\sqrt{x}>1\)
hay x>1
Kết hợp ĐKXĐ,ta được: x>1
Vậy: Để P>0 thì x>1

ĐKXĐ:
\(\left\{{}\begin{matrix}2-\sqrt{x}\\2+\sqrt{x}\\x-4\end{matrix}\right.\ne0\Leftrightarrow x\ne4\)
P=\(\dfrac{\left(2+\sqrt{x}\right)\left(2+\sqrt{x}\right)-\left(2-\sqrt{x}\right)\left(2-\sqrt{x}\right)+4x}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\)
P=\(\dfrac{\left(4+4\sqrt{x}+x\right)-\left(4-4\sqrt{x}+x\right)+4x}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\)
P=\(\dfrac{4+4\sqrt{x}+x-4+4\sqrt{x}-x+4x}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\)
P=\(\dfrac{8\sqrt{x}+4x}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\)
P=\(\dfrac{4\sqrt{x}\left(2+\sqrt{x}\right)}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\\ P=\dfrac{4\sqrt{x}}{2-\sqrt{x}}\)
b) Th P>0
<=> \(\dfrac{4\sqrt{x}}{2-\sqrt{x}}\)>0<=>\(4\sqrt{x}\)>0 <=> x>0(x\(\ne\)4)
TH P < 0
<=>\(\dfrac{4\sqrt{x}}{2-\sqrt{x}}\)<0 <=>\(4\sqrt{x}\)<0<=> \(\sqrt{x}< 0\)(vô lý)
c) |P|=1
=>P=1 hoặc P=-1
TH P=1
=>\(\dfrac{4\sqrt{x}}{2-\sqrt{x}}\)=1 <=> \(4\sqrt{x}\)=\(2-\sqrt{x}\) <=> x=\(\dfrac{4}{25}\)
TH P= -1
=>\(\dfrac{4\sqrt{x}}{2-\sqrt{x}}\)=-1<=> \(4\sqrt{x}\)=\(\sqrt{x}-2\)<=> \(\sqrt{x}=-\dfrac{2}{3}\)(vô lý)

A=\(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\)
ĐKXĐ :x\(\ne\)9,x\(\ge\)0
<=> \(\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)+2\sqrt{x}\left(\sqrt{x}+3\right)-3x-9}{x-9}\)
=\(\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{x-9}\)
=\(\dfrac{3\sqrt{x}-9}{x-9}\)=\(\dfrac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}=\dfrac{3}{\sqrt{x}+3}\)
ta có : A=1/3 => \(\dfrac{3}{\sqrt{x}+3}=\dfrac{1}{3}=>\sqrt{x}+3=9\)
=> x=36
vậy giá trị của x=36 khi A=1/3
B=\(\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{\sqrt{x}}{x-1}\right):\dfrac{1}{\sqrt{x}+1}\)
ĐKXĐ: x\(\ne\)1 ,x\(\ge\)0
<=> \(\dfrac{\sqrt{x}+1-\sqrt{x}}{x-1}:\dfrac{1}{\sqrt{x}+1}\)
=\(\dfrac{1}{x-1}:\dfrac{1}{\sqrt{x}+1}=\dfrac{\sqrt{x}+1}{x-1}=\dfrac{1}{\sqrt{x}-1}\)
ta có : B<0 =>\(\dfrac{1}{\sqrt{x}-1}< 0\)
=> 1< \(\sqrt{x}-1\)=> \(\sqrt{x}\)>2=>x>4
vậy x>4 khi B<0
\(ĐKXĐ:x\ne9\Rightarrow A=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9} =\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{x-9}+\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)}{x-9}+\dfrac{3x+9}{x-9}=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}=\dfrac{3\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3}{\sqrt{x}+3}\)

a: ĐKXĐ: x>0; x<>4
\(P=\left(2-\sqrt{x}+2\right)\cdot\dfrac{1}{\sqrt{x}-2}=\dfrac{4-\sqrt{x}}{\sqrt{x}-2}\)
b: P=2/3
=>(4-căn x)/(căn x-2)=2/3
=>2căn x-4=12-3căn x
=>5căn x=16
=>x=256/25
c: Khi x=8-2căn 7 thì \(P=\dfrac{4-\sqrt{7}+1}{\sqrt{7}-1-2}=\dfrac{5-\sqrt{7}}{\sqrt{7}-3}=-4-\sqrt{7}\)

a, \(P=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{2+5\sqrt{x}}{4-x}\)ĐK : \(x\ge0;x\ne4\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)+2\sqrt{x}\left(\sqrt{x}-2\right)-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
b, Ta có :
\(P=2\Rightarrow\dfrac{3\sqrt{x}}{\sqrt{x}+2}=2\Rightarrow3\sqrt{x}=2\sqrt{x}+4\Leftrightarrow\sqrt{x}=4\Leftrightarrow x=16\)( tmđk )
Vậy P = 2 thì x = 16

Điều kiện: x>2
P= \(\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{\sqrt{2}+2}{\sqrt{x}-1}\right)\)
P= \(\left(\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\dfrac{x-1-x+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\right)\)
P= \(\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}{3}\)
P= \(\dfrac{\sqrt{x}-2}{3\sqrt{x}}\)
b) P= \(\dfrac{1}{4}\)
⇔\(\dfrac{\sqrt{x}-2}{3\sqrt{x}}\) =\(\dfrac{1}{4}\)
⇔\(4\sqrt{x}-8=3\sqrt{x}\)
⇔\(\sqrt{x}=8\)
⇔x=64 (TM)
Vậy X=64(TMĐK) thì P=\(\dfrac{1}{4}\)

a: \(=\dfrac{x-\sqrt{x}-2-x-\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2\cdot\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(x-1\right)^2}{2}\)
\(=-\sqrt{x}\left(\sqrt{x}-1\right)\)
b: Để P<0 thì -(căn x-1)<0
=>căn x-1>0
=>x>1
c: \(P=-x+\sqrt{x}-\dfrac{1}{4}+\dfrac{1}{4}=-\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{1}{4}< =\dfrac{1}{4}\)
Dấu = xảy ra khi x=1/4

a: ĐKXĐ: x>=0; x<>1
b: \(P=\left(\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\right)\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{2}\)
\(=\dfrac{x-\sqrt{x}-2-\left(x+\sqrt{x}-2\right)}{\left(\sqrt{x}+1\right)^2\cdot\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{2}\)
\(=\dfrac{x-\sqrt{x}-2-x-\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\cdot\dfrac{\sqrt{x}-1}{2}\)
\(=\dfrac{-\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)^2}\)
c: Để P>0 thì \(\sqrt{x}-1< 0\)
=>0<x<1

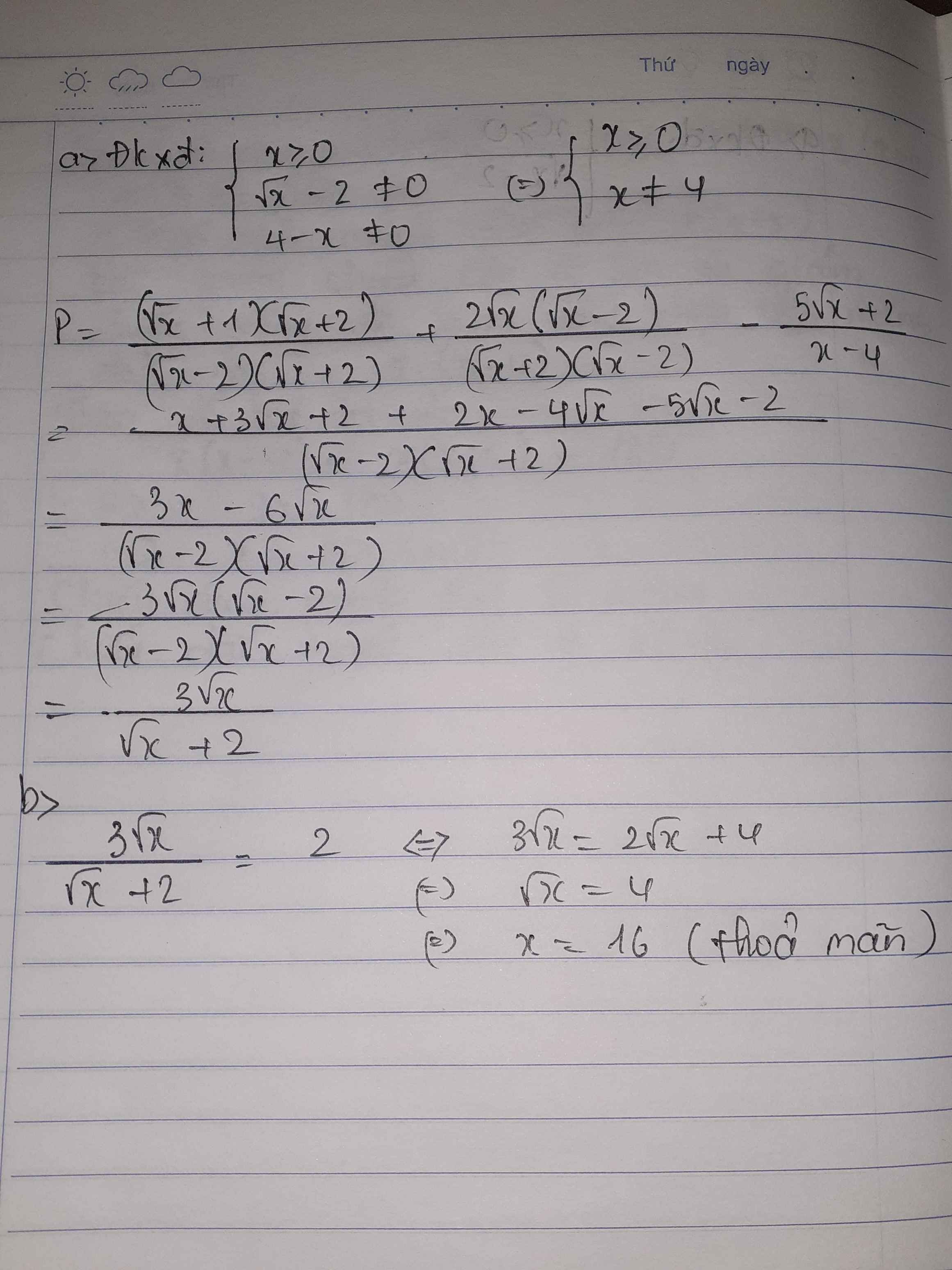
ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne2\end{matrix}\right.\)
\(M=\dfrac{\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{\left(\sqrt{x}+2\right)^2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(M=\dfrac{-8\sqrt{x}}{x-4}\)
\(M< 0\Leftrightarrow-\dfrac{8\sqrt{x}}{x-4}< 0\Leftrightarrow x-4>0\Leftrightarrow x>4\)