Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt tên các bộ ba lần lượt là A, B, ... như sau:
111 (A), 112 (B), 113 (C), 121 (D), 122 (E), 123 (F), 131 (G), 132 (H), 133 (I), 211 (J), 212 (K), 213 (L), 221 (M), 222 (N), 223 (O), 231 (P), 232 (Q), 233 (R), 311 (S), 312 (T), 313 (U), 321 (V), 322 (X), 323 (Y), 331 (Z), 332 (W), 333 (@)
Ta cần tìm dãy ngắn nhất chứa tất cả 27 bộ ba trên. Để tìm được dãy như vậy, ta sắp xếp lại các bộ ba trên sao cho hai chữ số cuối của bộ ba trước trùng với hai chữ số đầu của bộ ba sau. Một ví dụ là:
111 (A) , 112 (B), 121 (D), 211 (J), 113 (C), 131 (G), 312 (T), 122 (E), 221 (M), 212 (K), 123 (F), 231 (P), 313 (U), 132 (H), 321 (V), 213 (L), 133 (I), 332 (W), 322 (X), 222 (N), 223 (O), 232 (Q), 323 (Y), 233 (R), 333 (@), 331 (Z), 311 (S)
Sau đó loại bỏ 2 chữ số trùng nhau của các bộ ba kề nhau:
111, 112, 121, 211, 113, 131, 312, 122, 221, 212, 123, 231, 313, 132, 321, 213, 133, 332, 322, 222, 223, 232, 323, 233, 333, 331, 311
Cuối cùng ta được dãy 29 chữ số sau chứa tất cả các bộ ba có thể có của mật khẩu ba chữ số:
11121131221231321332223233311
Chú ý: dãy 29 chữ số không phải là duy nhất, tùy thuộc vào bộ ba đầu tiên và cách sắp xếp của mỗi người.
Đặt tên các bộ ba lần lượt là A, B, ... như sau:
111 (A), 112 (B), 113 (C), 121 (D), 122 (E), 123 (F), 131 (G), 132 (H), 133 (I), 211 (J), 212 (K), 213 (L), 221 (M), 222 (N), 223 (O), 231 (P), 232 (Q), 233 (R), 311 (S), 312 (T), 313 (U), 321 (V), 322 (X), 323 (Y), 331 (Z), 332 (W), 333 (@)
Ta cần tìm dãy ngắn nhất chứa tất cả 27 bộ ba trên. Để tìm được dãy như vậy, ta sắp xếp lại các bộ ba trên sao cho hai chữ số cuối của bộ ba trước trùng với hai chữ số đầu của bộ ba sau. Một ví dụ là:
111 (A) , 112 (B), 121 (D), 211 (J), 113 (C), 131 (G), 312 (T), 122 (E), 221 (M), 212 (K), 123 (F), 231 (P), 313 (U), 132 (H), 321 (V), 213 (L), 133 (I), 332 (W), 322 (X), 222 (N), 223 (O), 232 (Q), 323 (Y), 233 (R), 333 (@), 331 (Z), 311 (S)
Sau đó loại bỏ 2 chữ số trùng nhau của các bộ ba kề nhau:
111, 112, 121, 211, 113, 131, 312, 122, 221, 212, 123, 231, 313, 132, 321, 213, 133, 332, 322, 222, 223, 232, 323, 233, 333, 331, 311
Cuối cùng ta được dãy 29 chữ số sau chứa tất cả các bộ ba có thể có của mật khẩu ba chữ số:
11121131221231321332223233311
Chú ý: dãy 29 chữ số không phải là duy nhất, tùy thuộc vào bộ ba đầu tiên và cách sắp xếp của mỗi người.

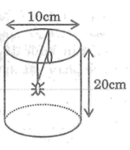
Khai triển hình trụ theo một đường sinh và trải phẳng ra ta được một hình chữ nhật có chiều rộng 20cm ,chiều dài bằng chu vi đáy của cái lọ: 10.3,14=31,4 (cm)
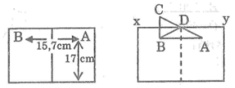
Theo đề bài, khi con kiến ở điểm A (hình dưới) cách đáy 17cm thì giọt mật ở điểm B cũng cách đáy 17cm.Khi đó con kiến cách giọt mật một khoảng cách bằng nửa chu vi đáy của cái lọ: 31,4 : 2 = 15,7 (cm)
Dựng điểm C đối xứng với B qua đường xy ,nối AC cắt xy tại D.Điểm D là điểm con kiến bò qua miệng của cái lọ đê vào bên trong thì đoạn đường BDA là ngắn nhất
Khai triển hình trụ theo một đường sinh và trải phẳng ra ta được một hình chữ nhật có chiều rộng 20cm ,chiều dài bằng chu vi đáy của cái lọ: 10.3,14=31,4 (cm)

chứ câu hỏi của bn bn xem linh tinh ko mà nói ghét nhất là linh tinh!!!
768769780-90

kết quả là 5 phút vì:
1 phút đầu thì rán 1 mặt của 4 cái đầu trước
phút thứ 2 thì ran 1 mặt cua 4 cai tiep theo
phut thu 3 thi ran thi ran 1 mat cua 2 cai cuoi va mat 2 cua 2 cai trong 4 cai dau
phut thu 4 thi ran 2 cai con lai trong 4 cai dau va 2 cai trong 4 cai tiep theo
phut thu 5 thi ran 2 cai trong 4 cai tiep theo va 2 cai cuoi

G/s (P),(d),(d1) cùng đi qua một điểm
Gọi I(a,b) là giao điểm của (P),(d),(d1)
Có \(I\in\left(P\right),\left(d\right),\left(d1\right)\)\(\Rightarrow\left\{{}\begin{matrix}b=a^2\left(1\right)\\b=a+2\left(2\right)\\b=-a+m\left(3\right)\end{matrix}\right.\)
Từ (1);(2)\(\Rightarrow a^2=a+2\)
\(\Leftrightarrow\left[{}\begin{matrix}a=2\\a=-1\end{matrix}\right.\)
TH1: Tại \(a=2\Rightarrow b=a^2=4\)
Thay \(a=2;b=4\) vào (3) ta được:\(4=-2+m\) \(\Leftrightarrow m=6\)
TH2: Tại \(a=-1\Rightarrow b=a^2=1\)
Thay \(a=-1;b=1\) vào (3) ta được:\(1=1+m\) \(\Leftrightarrow m=0\)
Vậy m=6 hoặc m=0
Phương trình hoành độ giao điểm của (d) và (P):
\(x^2=x+2\)
\(\Leftrightarrow x^2-x-2=0\)(*)
Ta có: \(a-b+c=1-\left(-1\right)+\left(-2\right)=0\)
Do đó phương trình (*) có 2 nghiệm phân biệt
\(x_1=-1;x_2=\dfrac{-c}{a}=2\)
\(x_1=-1\) thì \(y_1=x_1^2=\left(-1\right)^2=1\)
\(x_2=2\) thì \(y_2=x_2^2=2^2=4\)
Vậy (d) và (P) cắt nhau tại 2 điểm phân biệt \(A\left(-1;1\right);B\left(2;4\right)\)
Do đó các đồ thị của (P), (d) và \(\left(d_1\right)\)cùng đi qua 1 điểm
\(\Leftrightarrow\left[{}\begin{matrix}A\in\left(d_1\right)\\B\in\left(d_1\right)\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}1=1+m\\4=-2+m\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=6\end{matrix}\right.\)
Vậy khi m=0 hoặc m=6 thì các đồ thị của (P),(d) và cùng đi qua 1 điểm
-Chúc bạn học tốt-

Ta tìm được số còn lại ở hàng ngang thứ hai là: 14 - 9 - 2 = 3.
Vậy các số có thể tiếp tục dùng là : 1, 4, 5, 6, 7, 8.
Ở cột thứ hai, tổng hai ô còn lại bằng 6 nên hai số có thể điền là 5 và 1.
Trường hợp 1:
Các số còn lại: 4,6,7,8
2 số còn lại của cột 3 có tổng bằng 12 nên nó có thể là 4 và 8. 8 phải ở hàng thứ ba vì 5 > 1.
Từ đó ta hoàn thiện được bảng:
Trường hợp 2:
Các số còn lại: 4,6,7,8
2 số còn lại của cột 3 có tổng bằng 12 nên nó có thể là 4 và 8. 8 phải ở hàng thứ nhất vì 5 > 1.
Từ đó ta hoàn thiện được bảng: