Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)

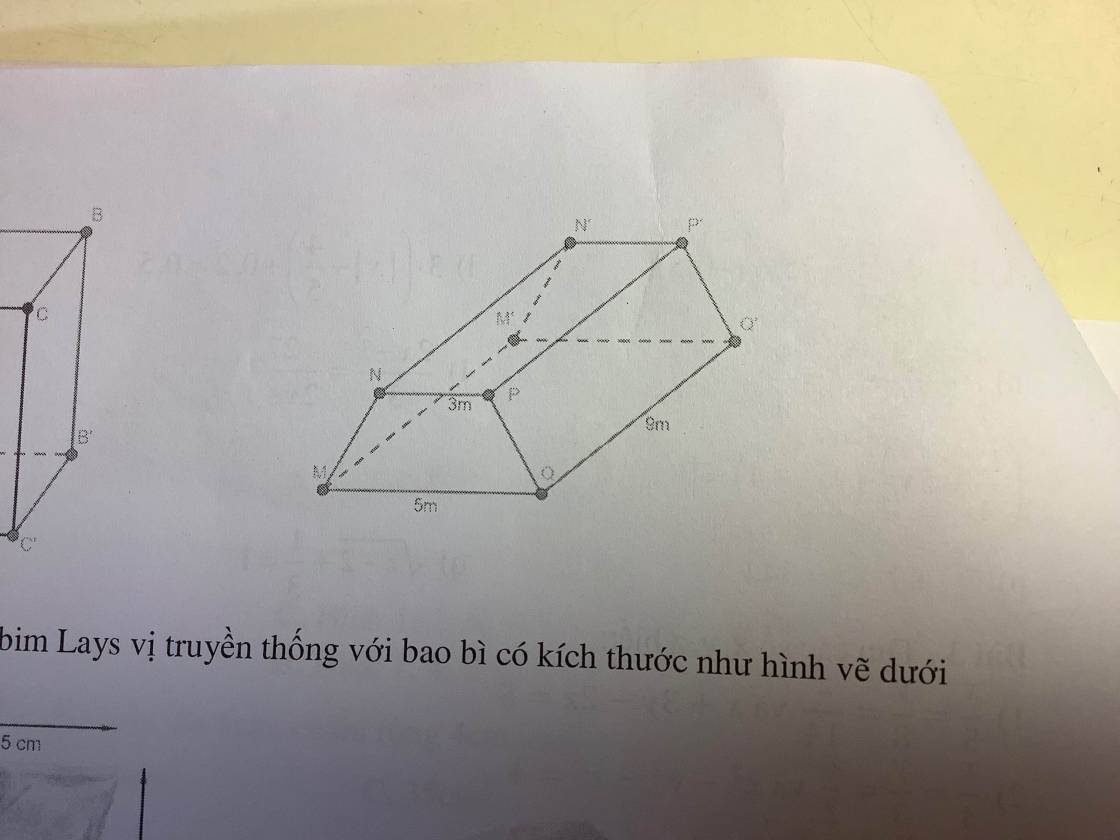
Chu vi đáy hình lăng trụ đứng đó là:
4+5+6=15 (cm)
Diện tích xung quanh hình lăng trụ đứng đó là:
Sxq = 15.10 = 150 (cm2 )
b)
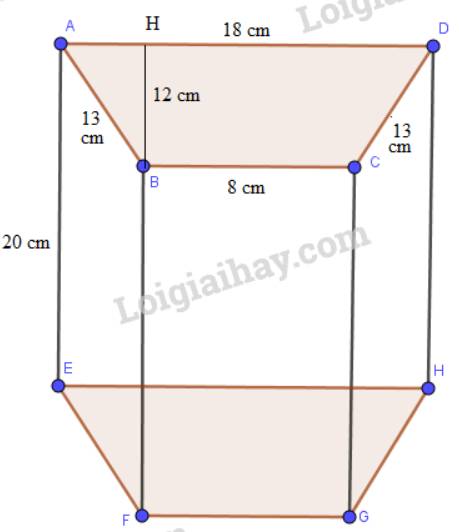
Chu vi đáy là: 8+18+13+13 = 52 (cm)
Diện tích đáy là: Sđáy = (8+18).12:2 = 156 (cm2)
Diện tích toàn phần của lăng trụ đó là:
Stp = Sxq + 2. Sđáy = 52. 20 +2. 156 = 1352 (cm2)
cho tam giác mnp có mn= 4cm np=1cm và độ dài của canhk mp là một số nguyên (cm). tính độ dài cạnh mp

có : MN+NP < MP < MN-NP ( Bất đẳng thức tam giác )
4+1 < MP < 4-1
5 < MP < 3
=> MP =4 ( cm)

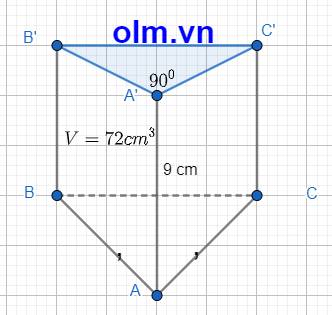
VABCA'B'C' = SABC.h
Diện tích của tam giác ABC là: 72 : 9 = 8 (cm2)
SABC = \(\dfrac{1}{2}\)AB.AC = \(\dfrac{1}{2}\)AB2 = 8 ⇒ AB2 = 8.2 = 16
⇒ AB = AC = \(\sqrt{16}\) = 4 (cm)
Vậy độ dài cạnh đáy AB dài 4cm

tự kẻ hình nha
a) xét tam giác BAN và tam giác BAP có
AB chung
BAN=BAP(=90 độ)
NA=AP(gt)
=> tam giác BAN= tam giác BAP(cgc)
=> BNA=BPA(hai góc tương ứng)
=> tam giác BNP cân B=> BN=BP
b) xét tam giác BMN và tam giác BCP có
NB=BP(cmt)
BMN=BCP(=90 độ)
MBN=CBP( đối đỉnh)
=> tam giác BMN= tam giác BCP(ch-gnh)
c) từ tam giác BAN=BAP=> NBA=PBA( hai cạnh tương ứng)
từ tam giác BMN= tam giác BCP=> MB=BC( hai cạnh tương ứng)
xét tam giác BMA và tam giác BCA có
MB=BC(cmt)
MBA=CBA(=CBP+PBA)
AB chung
=> tam giác BMA= tam giác BCA(cgc)
=> MAB=CAB(hai góc tương ứng)
=> AB là p/g của MAC