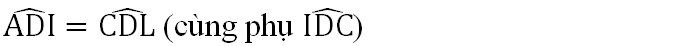Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác vuông ADI vuông tại A và tam giác CDL vuông tại C có:
AD = CD (cạnh hình vuông)
Nên ΔADI = ΔCDL (g.c.g)
\(\Rightarrow\) DI = DL
Trong tam giác DKL vuông tại D với đường cao DC. Theo định lí 4, ta có: \(\frac{1}{DL^2}+\frac{1}{DK^2}=\frac{1}{DC^2}\)
Mà: DI = DL (cmt)
\(\Rightarrow\) \(\frac{1}{DI^2}+\frac{1}{DK^2}=\frac{1}{DC^2}\) (đpcm)

a, Xté tứ giác AMIN có :
BMI=MAN=INA=900
=> Tứ giác AMIN là hình chữ nhật
b, Xét ΔABC
có : BI=IC ( gt)
IN // AM ( gt )
=> AN=NC
mà IN=ND
=> Tứ giác ADCI là hình bình hành (1)
mà INC = 900 (2) Từ (1) và (2) => ADCI là hình thoi
c, Kẻ IQ // BK (QϵCD)
ΔBKC có :
BI = IC (gt)
IQ // BK (cách dựng )
cm tương tự : DK=KQ
=> DK=KQ=QC
=> DK/DC = 1/3