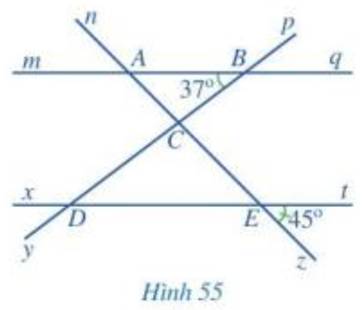
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

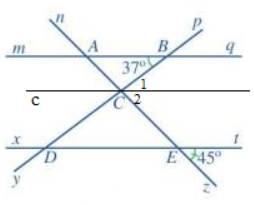
a) Các cặp góc đồng vị bằng nhau là: góc mAn và xEn; góc mAz và xEz; góc nAq và nEt; góc qAz và tEz; góc pBq và pDt; góc qBy và tDy; góc mBy và xDy; góc pBm và pDx
b) Vì mq // xt nên \(\widehat {BAC} = \widehat {zEt}\) ( 2 góc đồng vị) nên \(\widehat {BAC} = 45^\circ \).
Vì mq // xt nên \(\widehat {CDE} = \widehat {ABC}\) ( 2 góc so le trong) nên \(\widehat {CDE} = 37^\circ \).
c)
Bạn Nam nói đúng vì:
Vì c // mq nên \(\widehat {ABC} = \widehat {{C_1}}\) ( 2 góc so le trong) nên \(\widehat {{C_1}} = 37^\circ \)
Vì c // xt nên \(\widehat {CED} = \widehat {{C_2}}\) ( 2 góc so le trong) nên \(\widehat {{C_2}} = 45^\circ \)
Vì \(\widehat {{C_1}} + \widehat {{C_2}} = \widehat {BCE}\) nên \(\widehat {BCE} = \widehat {{C_1}} + \widehat {{C_2}} = 37^\circ + 45^\circ = 82^\circ \)

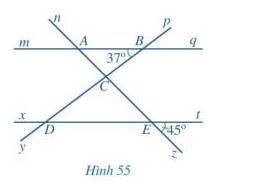
a, Các góc đồng vị bằng nhau là:
\(\widehat{nAm}\) = \(\widehat{AEx}\); \(\widehat{mAE}\) = \(\widehat{zED}\); \(\widehat{nAB}\) = \(\widehat{AEt}\)
\(\widehat{qAE}\) = \(\widehat{tEz}\); \(\widehat{pBq}\) = \(\widehat{BDE}\); \(\widehat{qBC}\) = \(\widehat{EDy}\); \(\widehat{pBA}\) = \(\widehat{BDx}\); \(\widehat{ABD}\)=\(\widehat{xDy}\)
b, Các góc so le trong:
\(\widehat{ABC}\) = \(\widehat{CDE}\); \(\widehat{mAC}\) = \(\widehat{CEt}\); \(\widehat{BAC}\) = \(\widehat{CED}\); \(\widehat{qBc}\) = \(\widehat{CDx}\)
c, \(\widehat{BAC}\) = \(\widehat{zEt}\) = 450
\(\widehat{CDE}\) = \(\widehat{ABC}\) = 390
d, \(\widehat{BCE}\) = \(\widehat{CDE}\) + \(\widehat{CED}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó.
\(\widehat{CED}\) = \(\widehat{zEt}\) = 450 (hai góc đối đỉnh)
\(\widehat{BCE}\) = 390 + 450 = 840

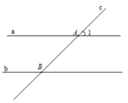
\(a,\)So le trong: \(E_1 và F_2;E_2 và F_1\)
Đồng vị: \(E_1 và F_4;E_2 và F_3;E_3 và F_2;E_4 và F_1\)
Trong cùng phía: \(E_1 và F_1;E_2 và F_2\)
\(b,\widehat{F_1}=\widehat{F_3}=120^0\left(đối.đỉnh\right)\\ \widehat{F_2}+\widehat{F_3}=180^0\left(kề.bù\right)\Rightarrow\widehat{F_2}=180^0-120^0=60^0\\ \widehat{F_2}=\widehat{F_4}-60^0\left(đối.đỉnh\right)\)
\(c,C_1:\widehat{F_2}=\widehat{E_3}\left(=60^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên \(a//b\)
\(C_2:\)\(\widehat{E_1}=\widehat{E_3}=60^0\left(đối.đỉnh\right)\Rightarrow\widehat{E_1}=\widehat{F_2}\left(=60^0\right)\)
Mà 2 góc này ở vị trí so le trong nên \(a//b\)
a. Các cặp góc:
- So le trong là: \(\widehat{E_1}\) và \(\widehat{F_2};\widehat{E_2}\) và \(\widehat{F_1}\)
- Đồng vị là: \(\widehat{E_4},\widehat{F_1};\widehat{E_3},\widehat{F_2};\widehat{E_2},\widehat{F_3};\widehat{E_1},\widehat{F_4}\)
- Trong cùng phía là: \(\widehat{E_1},\widehat{F_1};\widehat{E_2},\widehat{F_2}\)
b. Ta có: \(\widehat{F_1}=\widehat{F_3}=120^o\) (đối đỉnh)
\(\widehat{F_2}=180^o-\widehat{F_1}=180^o-120^o=60^o\)
\(\widehat{F_3}=120^o\)
\(\widehat{F_4}=\widehat{F_2}=60^o\) (đối đỉnh)
c.
C1: Ta có: \(\widehat{E_1}=\widehat{E_3}=60^o\) (đối đỉnh)
Ta thấy: \(\widehat{E_1}=\widehat{F_2}=60^o\)
=> a//b (so le trong)
C2: Ta có: \(\widehat{E_2}=180^o-\widehat{E_3}=180^o-60^o=120^o\)
Ta thấy: \(\widehat{E_2}=\widehat{F_1}=120^o\)
=> a//b (so le trong)

* Góc đồng vị với A 1 ^ bằng 30o, khác A 1 ^ nên b1 không song song với a.
Vậy b1 không trùng với b.
* Góc kề bù với góc đồng vị của A 1 ^ bằng 145o nên góc
đồng vị với A 1 ^ bằng 180o – 145o = 35o = A 1 ^ .
Vậy b2 song song với a nên b2 trùng với b (theo tiên đề Ơ-clit)

Lời giải chi tiết
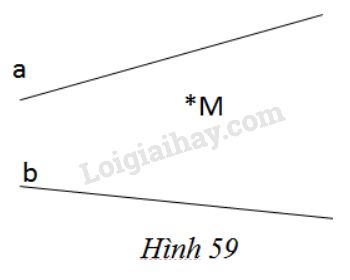
a) Trước hết, ta nêu cách vẽ một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
1. Cách vẽ dùng ê ke và thước kẻ:
+ Cho trước đường thẳng p và M ∉ p.
Đặt một lề ê ke trùng với p, dịch chuyển ê ke trên p sao cho lề thứ hai của ê ke sát vào M
+ Cho trước đường thẳng p và M∈pM∈p
Đặt một lề ê ke trùng với p và dịch chuyển ê ke trên p sao cho góc ê ke trùng với M.
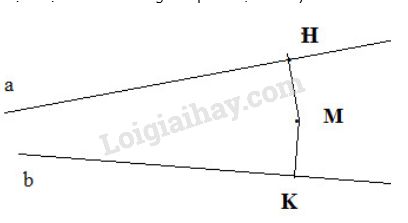
2. Cách vẽ dùng compa và thước kẻ:
+ Cho trước đường thẳng p và M ∉ p.
Vẽ đường thẳng qua M vuông góc với p.
Chọn trên p hai điểm A và B.
Vẽ các đường tròn (A; AM) và (B; BM)
Hai đường tròn này cắt nhau tại M và M’ thì NM’ vuông góc với p
Chú ý: Có thể xem bài tập 51 phần hình học. Cho trước đường thẳng p và
Vẽ đường thẳng vuông góc với p tại M
Dùng compa vẽ đường tròn (M; r1) cắt p tại A và B. Vẽ các đường tròn (A;r2) và (B; r2) với r2 > r1.
Các đường tròn này cắt nhau tại E và F thì đường thẳng EF vuông góc p tại M. Bây giờ ta theo một trong hai cách vẽ nêu trên vẽ đường thẳng qua M vuông góc a tại H và đường thẳng qua M vuông góc với b tại K
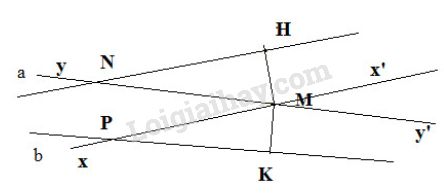
b) Vẽ đường thẳng xx’ vuông góc với MH tại M và đường thẳng yy’ vuông góc với MK tại M thì xx’ // a (vì cùng vuông góc với MH) và yy’ //b.
c) Giả sử a cắt yy’ tại N và b cắt xx’ tại P.
Một số cặp góc bằng nhau là góc x'My' và x'Pk , HNM và MPK
Một số cặp góc bù nhau, chẳng hạn như góc HNM và nMx' , kPm và pMy'
Hình vẽ đâu rồi bạn?