Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

 giải
giải
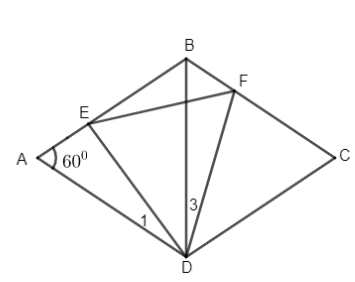
ta có AB=AD(gt)và góc A=60 độ nên tam giác DEF đều=>BD=AD
Tương tự tam giác DEF đều =>góc CBD=60độ
Từ BE+BF=BD=>AE=BF
Xét tam giác AED và tam giác BFD có:
AD=BD(cmt)
góc A=góc CBD=60 độ
AE=BF
Do đó tam giác AED=tam giác BFD(c,g.c)
=>DE=DF
nên tam giác DEF cân (1)
Và góc D1=góc D3 nên góc D1+góc EBD=60độ =>góc D3+góc EBD=60độ (2)
Từ (1) và (2) suy ra tam giác DEF đều.

Câu hỏi của pham trung thanh - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo lời giải tại link trên nhé.

1. Ta có tam giác ABC cân tại A, do đó AB = AC.
Gọi I là giao điểm của đường phân giác góc B và đường phân giác góc C.
Ta cần chứng minh MN // BC.
Ta có:
∠BIM = ∠CIM (do I nằm trên đường phân giác góc B và đường phân giác góc C)
∠BIM = ∠CIM = ∠BIC/2 (do I nằm trên đường phân giác góc B và đường phân giác góc C)
∠BIC = ∠BAC (do tam giác ABC cân tại A)
∠BIC = ∠BAC = ∠BCA (do tam giác ABC cân tại A)
Do đó, ta có ∠BIM = ∠CIM = ∠BCA.
Từ đó, ta có MN // BC (do ∠MNI = ∠BCA và ∠MIN = ∠BAC).
Vậy ta đã chứng minh MN // BC.
2. a) Ta có BF/BE = 2/3.
Gọi x là độ dài của BE.
Do BF/BE = 2/3, ta có BF = (2/3)x.
Gọi y là độ dài của FE.
Do FE = 12cm, ta có y = 12cm.
Gọi z là độ dài của IF.
Do I là giao điểm của FE và BD, ta có IF/FE = BD/BE.
Do đó, IF/12 = BD/x.
Ta có BD = BC + CD = BC + BA = BC + BE.
Do đó, IF/12 = (BC + BE)/x.
Ta có BF/BE = 2/3, nên BF = (2/3)x.
Do đó, BC = BF + FC = (2/3)x + (1/3)x = x.
Vậy, IF/12 = (x + x)/x = 2.
Từ đó, ta có IF = 2 * 12 = 24cm.
Do đó, IE/IF = BE/FE = x/12.
Vậy, IE/IF = x/12.
b) Giả sử FE = 12cm.
Từ phần a), ta đã tính được IF = 24cm.
Do đó, IE/IF = x/12.
Ta cần tính x.
Ta có BF/BE = 2/3, nên BF = (2/3)x.
Do BF = (2/3)x và BC = x, ta có BC = BF + FC.
Do đó, x = (2/3)x + FC.
Từ đó, FC = (1/3)x.
Vậy, BC = BF + FC = (2/3)x + (1/3)x = x.
Do đó, BC = x = 12cm.
Vậy, độ dài của IE và IF lần lượt là 12cm và 24cm.

a, hình vuông có thể là hcn mà bn vì nó đều có 4 góc bằng nhau và 2 cạnh đối song song bằng nhau
1: Xét tứ giác ABCD có
góc BAD=góc ABC=góc BCD=90 độ
=>ABCD là hình chữ nhật

Ta có ABCD là hình thoi nên \(AD=AB\)
Mà \(\widehat{A}=60^0\) nên ABD đều
Lại có BD là phân giác \(\widehat{ABC}\Rightarrow\widehat{ABD}=\widehat{DBC}=60^0\)
\(\left\{{}\begin{matrix}BE+BF=BD=AB\\AE+BE=AB\end{matrix}\right.\Rightarrow AE=BF\)
\(\left\{{}\begin{matrix}AE=BF\\AD=BD\\\widehat{DAE}=\widehat{DBF}=60^0\end{matrix}\right.\Rightarrow\Delta DEA=\Delta DFB\left(c.g.c\right)\\ \Rightarrow DE=DF\)
Do đó DEF cân tại D
Mà \(\widehat{ADE}=\widehat{BDF}\left(\Delta DEA=\Delta DFB\right)\)
\(\Rightarrow\widehat{ADE}+\widehat{EDB}=\widehat{BDF}+\widehat{EDB}\\ \Rightarrow\widehat{ADB}=\widehat{EDF}=60^0\)
Vậy tam giác DEF đều