Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xét ΔBAC có BA=BC và góc B=60 độ
nên ΔBAC đều
=>AE vuông góc với BC và góc EAC=60/2=30 độ
Xét ΔDAC có DA=DC và góc D=60 độ
nên ΔDAC đều
=>AF vuông góc với CD và góc FAC=60/2=30 độ
Xét ΔAEC vuông tại E và ΔAFC vuông tại F có
AC chung
góc EAC=góc FAC
Do đó: ΔAEC=ΔAFC
=>AE=AF
mà góc FAE=60 độ
nên ΔAEF đều
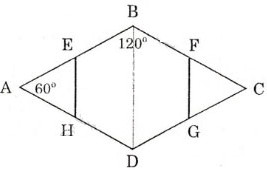
ABCD là hình thoi, 
= 
nên 
= 
, 
= .
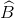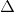EAH là tam giác đều (vì tam giác cân có một góc ) nên 
= , 
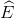= . Cũng thế 
= , 
= .
Vậy EBFGDH có tất cả các góc bằng nhau, mặt khác EBFGDH cũng có tất cả các cạnh bằng nhau( bằng nửa cạnh hình thoi)
Vậy EBFGDH là một lục giác đều
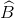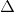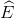ABCD là hình thoi, = nên = , = .EAH là tam giác đều (vì tam giác cân có một góc ) nên = , = . Cũng thế = , = .
Vậy EBFGDH có tất cả các góc bằng nhau, mặt khác EBFGDH cũng có tất cả các cạnh bằng nhau( bằng nửa cạnh hình thoi)
Vậy EBFGDH là một lục giác đều
a) FN là đường trung bình của tam giác ADC
\(\Rightarrow FN=\frac{AD}{2}\)
EM là đường trung bình của tam giác ADB
\(\Rightarrow EM=\frac{AD}{2}\)
NE là đường trung bình của tam giác ABC
\(\Rightarrow EN=\frac{CB}{2}\)
FM là đường trung bình của tam giác BDC
\(\Rightarrow FM=\frac{CB}{2}\)
Mà AD = BC (gt)
\(\Rightarrow FN=EM=EN=FM=\frac{AD}{2}=\frac{CB}{2}\)
\(\Rightarrow FN=EM=EN=FM\)
=> Tứ giác FNEM là hình thoi
b) FM là đường trung bình của tam giác BDC
\(\Rightarrow FM//BC\Leftrightarrow\widehat{DFM}=\widehat{DCB}=80^o\)
FN là đường trung bình của tam giác ADC
\(\Rightarrow FN//AD\Leftrightarrow\widehat{CFN}=\widehat{CDA}=40^o\)
Ta có \(\widehat{CFN}+\widehat{MFN}+\widehat{DFM}=180^o\)
\(\Leftrightarrow40^o+\widehat{MFN}+80^o=180^o\Leftrightarrow\widehat{MFN}=60^o\)
Hình tự vẽ nhé , với lại chỉ ghi hướng cho nhan thôi chứ làm chi tiết lâu lắm
a)Chứng minh AG vuông góc với HF ( để ý góc D = 60 đỏồi tính toán các góc để có được góc = 90 độ)
Gọi FG giao với BD tại M, thì dễ dàng chứng minh được M là trung điểm của FG => IM là đường trung bình
=> IM //AG
Mà AG vuông góc với HF => IM vuông góc với HF
gọi PG giao với MH=O, thì dễ dàng chứng minh PHGM là hình chữ nhật => O là trung điểm của PG và HM
thì ta có tam giác HIM vuông tại I có O là trung điểm của HM => IO=1/2HM=1/2PG => tam giác PIG vuông tại I(ĐPCM)
hóng các cao nhân ý b ^_^
A B C D F E
ABCD là hình thoi => BAD = BCD = 1200
Mà AC là đường phân giác của BAD và BCD
=> FCA = ECA = 1200/2 = 600
Xét hình thoi ABCD có B + D = 3600 - 1200.2 = 1200
Mà B = D => B = D = 1200/2 = 600
Xét tam giác ADC có D = FCA => tam giác ADC cân tại A
mà AF là trung tuyến => AF đồng thời là phân giác => DAF = CAF
Chứng minh tương tự ta có CAE = BAE
Mà FAC = EAC ( vì AC là phân giác của FAE - tính chất đường chéo trong hình thoi )
Ta có : DAF + CAF + CAE + BAE = 1200
hay 2CAF + 2CAE = 1200
=> CAF + CAE = 120/2 = 600 (1)
Xét tam giác ADF = tam giác ABE ( c-g-c ) ( tự chứng minh )
=> AF = AE
=> tam giác AFE cân tại A (2)
Từ (1) và (2) => tam giác AFE cân ( đpcm )