Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(SA \bot \left( {ABCD} \right) \Rightarrow \left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
\(ABCD\) là hình vuông \( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = b\sqrt 2 \)
\(\cos \widehat {SCA} = \frac{{AC}}{{SC}} = \frac{1}{2} \Rightarrow \widehat {SCA} = {60^ \circ }\)
Vậy \(\left( {SC,\left( {ABCD} \right)} \right) = {60^ \circ }\)
Chọn A.

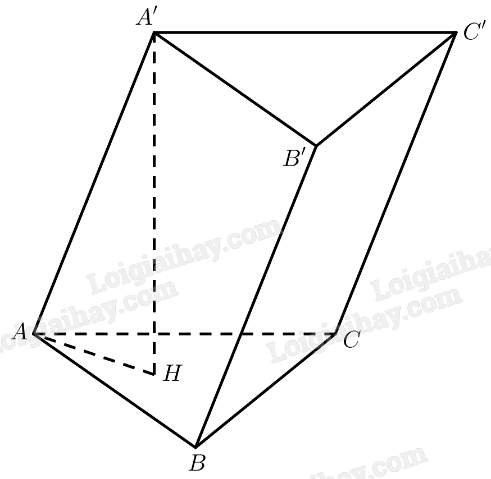
Gọi \(H\) là hình chiếu vuông góc của \(A'\) lên \(\left( {ABC} \right)\)
\(\begin{array}{l} \Rightarrow A'H \bot \left( {ABC} \right)\\ \Rightarrow \left( {AA',\left( {ABC} \right)} \right) = \left( {AA',AH} \right) = \widehat {A'AH}\end{array}\)
\(\Delta AA'H\) vuông tại \(H \Rightarrow A'H = AA'.\sin \widehat {A'AH} = \frac{{a\sqrt 3 }}{2}\)
Vì \(\left( {ABC} \right)\parallel \left( {A'B'C'} \right)\) nên \(d\left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) = d\left( {A',\left( {ABC} \right)} \right) = A'H = \frac{{a\sqrt 3 }}{2}\)

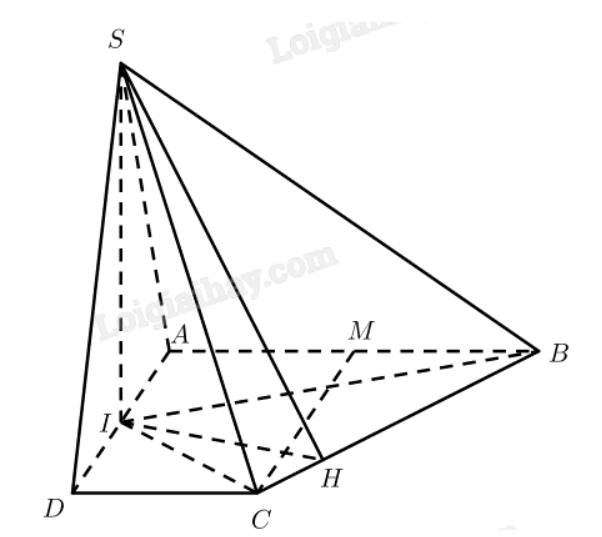
\(\left. \begin{array}{l}\left( {SBI} \right) \bot \left( {ABCD} \right)\\\left( {SCI} \right) \bot \left( {ABCD} \right)\\\left( {SBI} \right) \cap \left( {SCI} \right) = SI\end{array} \right\} \Rightarrow SI \bot \left( {ABCD} \right)\)
Kẻ \(IH \bot BC\left( {H \in BC} \right)\)
\(SI \bot \left( {ABCD} \right) \Rightarrow SI \bot BC\)
\( \Rightarrow BC \bot \left( {SIH} \right) \Rightarrow BC \bot SH\)
Vậy \(\widehat {AHI}\) là góc nhị diện \(\left[ {S,BC,A} \right]\)\( \Rightarrow \widehat {AHI} = {60^ \circ }\)
\(\begin{array}{l}{S_{ABC{\rm{D}}}} = \frac{1}{2}\left( {AB + C{\rm{D}}} \right).A{\rm{D}} = 3{a^2}\\AI = I{\rm{D}} = \frac{1}{2}A{\rm{D}} = a\\{S_{AIB}} = \frac{1}{2}AB.AI = {a^2},{S_{CI{\rm{D}}}} = \frac{1}{2}C{\rm{D}}.I{\rm{D}} = \frac{{{a^2}}}{2}\\ \Rightarrow {S_{BIC}} = {S_{ABC{\rm{D}}}} - {S_{AIB}} - {S_{CI{\rm{D}}}} = \frac{{3{a^2}}}{2}\end{array}\)
Gọi \(M\) là trung điểm của \(AB\)
\(\begin{array}{l} \Rightarrow BM = \frac{1}{2}AB = a,CM = AD = 2a \Rightarrow BC = \sqrt {B{M^2} + C{M^2}} = a\sqrt 5 \\ \Rightarrow IH = \frac{{2{{\rm{S}}_{BIC}}}}{{BC}} = \frac{{3a\sqrt 5 }}{5} \Rightarrow SI = IH.\tan \widehat {SHI} = \frac{{3a\sqrt {15} }}{5}\end{array}\)
\({V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SI = \frac{{3{a^3}\sqrt {15} }}{5}\)

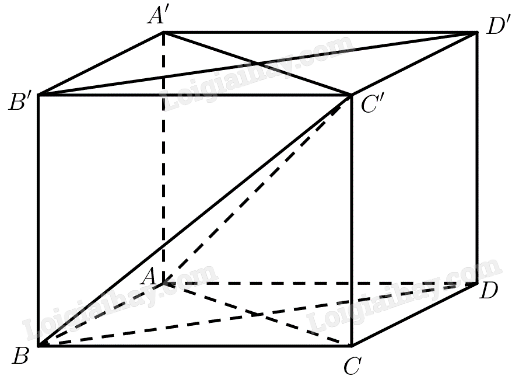
a) \(ABCD\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\(BB' \bot \left( {ABCD} \right) \Rightarrow BB' \bot AC\)
\(\left. \begin{array}{l} \Rightarrow AC \bot \left( {B{\rm{DD'B'}}} \right)\\AC \subset \left( {ACC'A'} \right)\end{array} \right\} \Rightarrow \left( {ACC'A'} \right) \bot \left( {B{\rm{DD}}'B'} \right)\)
b) \(ABCD\) là hình vuông \( \Rightarrow AB\parallel C{\rm{D}}\)
\(CDD'C'\) là hình chữ nhật \( \Rightarrow C{\rm{D}}\parallel C'{\rm{D}}'\)
\( \Rightarrow AB\parallel C'{\rm{D}}' \Rightarrow d\left( {AB,C'{\rm{D}}'} \right) = d\left( {B,C'{\rm{D}}'} \right)\)
\(A'B'C'D'\) là hình vuông \( \Rightarrow C'D' \bot B'C'\)
\(CDD'C'\) là hình chữ nhật \( \Rightarrow C'D' \bot CC'\)
\( \Rightarrow C'D' \bot \left( {BCC'B'} \right) \Rightarrow C'D' \bot BC' \Rightarrow d\left( {B,C'{\rm{D}}'} \right) = BC'\)
\(ABCD\) là hình vuông \( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
\(\begin{array}{l}CC' \bot \left( {ABCD} \right) \Rightarrow \left( {AC',\left( {ABCD} \right)} \right) = \left( {AC',AC} \right) = \widehat {CAC'} = {60^ \circ }\\ \Rightarrow CC' = AC.\tan \widehat {CAC'} = a\sqrt 6 \end{array}\)
\(\Delta BCC'\) vuông tại \(C \Rightarrow BC{'^2} = \sqrt {B{C^2} + CC{'^2}} = a\sqrt 7 \)
Vậy \(d\left( {AB,C'{\rm{D}}'} \right) = a\sqrt 7 \).

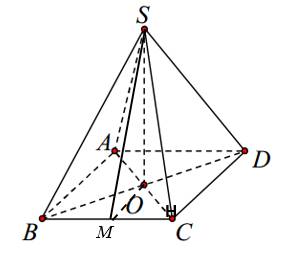
Gọi \(M\) là trung điểm \(BC\).
Ta có:\(OM=\dfrac{1}{2}.AB=2a;AC=\sqrt{AB^2+BC^2}=5a;OC=\dfrac{1}{2}AC=\dfrac{5}{2}a\)
\(SO=\sqrt{SC^2-OC^2}=\dfrac{5\sqrt{3}}{2}a\)
\(\left[S,BC,A\right]=\widehat{SMO}\)
\(\tan\widehat{SMO}=\dfrac{SO}{OM}=\dfrac{5\sqrt{3}}{4}\)
Suy ra:\(\widehat{SMO}=65,2^o\)
\(\Rightarrow D\)


a) Gọi \(I\) là trung điểm của \(BC\).
Tam giác \(ABC\) đều \( \Rightarrow AI \bot BC\)
Tam giác \(A'BC\) cân tại \(A' \Rightarrow A'I \bot BC\)
\( \Rightarrow \left( {\left( {A'BC} \right),\left( {ABC} \right)} \right) = \left( {A'I,AI} \right) = \widehat {AI{\rm{A}}'} = {60^ \circ }\)
Tam giác \(ABC\) đều \( \Rightarrow AI = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)
\( \Rightarrow AA' = AI.\tan \widehat {AI{\rm{A}}'} = \frac{{3a}}{2}\)
b) \({S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\)
\({V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{3{a^3}\sqrt 3 }}{8}\)


Kẻ \(OI \bot C{\rm{D}}\left( {I \in C{\rm{D}}} \right),OH \bot SI\left( {H \in SI} \right)\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SO \bot \left( {ABCD} \right) \Rightarrow SO \bot C{\rm{D}}\\OI \bot C{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {SOI} \right)\\\left. \begin{array}{l} \Rightarrow C{\rm{D}} \bot OH\\OH \bot SI\end{array} \right\} \Rightarrow OH \bot \left( {SC{\rm{D}}} \right)\\ \Rightarrow d\left( {O,\left( {SC{\rm{D}}} \right)} \right) = OH\end{array}\)
\(\Delta ABC\) đều \( \Rightarrow AC = a \Rightarrow OC = \frac{1}{2}AC = \frac{a}{2}\)
\(\Delta ABD\) có \(\widehat {BA{\rm{D}}} = {120^ \circ } \Rightarrow B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2} - 2{\rm{A}}B.A{\rm{D}}} = a\sqrt 3 \Rightarrow OD = \frac{1}{2}B{\rm{D}} = \frac{{a\sqrt 3 }}{2}\)
\(\Delta OCD\) vuông tại \(O\) có đường cao \(OI\)
\( \Rightarrow OI = \frac{{OC.O{\rm{D}}}}{{C{\rm{D}}}} = \frac{{a\sqrt 3 }}{4}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OI \Rightarrow \Delta SOI\) vuông tại \(O\) có đường cao \(OH\)
\( \Rightarrow OH = \frac{{SO.OI}}{{\sqrt {S{O^2} + O{I^2}} }} = \frac{{a\sqrt {51} }}{{17}}\)
Vậy \(d\left( {O,\left( {SCD} \right)} \right) = OH = \frac{{a\sqrt {51} }}{{17}}\).

a)
\(38^\circ = \frac{{\pi .38}}{{180}} = \frac{{19\pi }}{{90}}\,\,\,\left( {rad} \right)\)
b)
\( - 115^\circ = \frac{{\pi .\left( { - 115} \right)}}{{180}} = \frac{{ - 23\pi }}{{36}}\,\,\left( {rad} \right)\)
c)
\({\left( {\frac{3}{\pi }} \right)^\circ }= \frac{{\pi .\frac{3}{\pi }}}{{180}} = \frac{1}{{60}}\,\,\,\left( {rad} \right)\)

a) \(cos638^o=cos\left(-82^o\right)=cos\left(82^o\right)=sin8^o\)
b) \(cot\dfrac{19\pi}{5}=cot\dfrac{4\pi}{5}=-cot\dfrac{\pi}{5}\)
a) Đáp án:B
b) Đáp án:D
c) Đáp án:B
d) Đáp án:B