Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


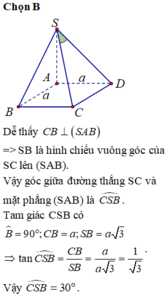
Dựng CH _|_ AB => CH _|_ (SAB)
Giả sử MN cắt AD tại F. Theo định lý Talet ta có:
\(\frac{DF}{MC}=\frac{ND}{NC}=\frac{1}{2}\Rightarrow DF=\frac{MC}{2}=\frac{a}{4}\)
Khi đó \(\frac{PA}{PC}=\frac{AF}{MC}=\frac{5}{2}\Rightarrow\frac{CA}{PA}=\frac{7}{5}\)
Do đó: d (P;(SAB))=\(\frac{5}{7}d\left(C;\left(SAB\right)\right)=\frac{5}{7}CH=\frac{5}{7}\cdot\frac{a\sqrt{3}}{2}=\frac{5a\sqrt{3}}{14}\)

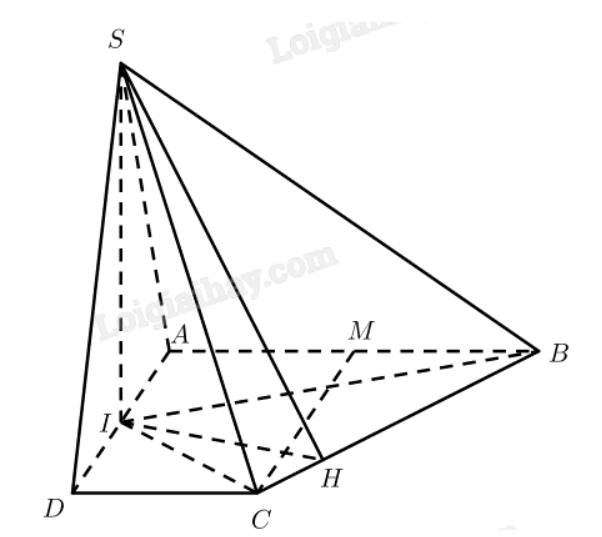
\(\left. \begin{array}{l}\left( {SBI} \right) \bot \left( {ABCD} \right)\\\left( {SCI} \right) \bot \left( {ABCD} \right)\\\left( {SBI} \right) \cap \left( {SCI} \right) = SI\end{array} \right\} \Rightarrow SI \bot \left( {ABCD} \right)\)
Kẻ \(IH \bot BC\left( {H \in BC} \right)\)
\(SI \bot \left( {ABCD} \right) \Rightarrow SI \bot BC\)
\( \Rightarrow BC \bot \left( {SIH} \right) \Rightarrow BC \bot SH\)
Vậy \(\widehat {AHI}\) là góc nhị diện \(\left[ {S,BC,A} \right]\)\( \Rightarrow \widehat {AHI} = {60^ \circ }\)
\(\begin{array}{l}{S_{ABC{\rm{D}}}} = \frac{1}{2}\left( {AB + C{\rm{D}}} \right).A{\rm{D}} = 3{a^2}\\AI = I{\rm{D}} = \frac{1}{2}A{\rm{D}} = a\\{S_{AIB}} = \frac{1}{2}AB.AI = {a^2},{S_{CI{\rm{D}}}} = \frac{1}{2}C{\rm{D}}.I{\rm{D}} = \frac{{{a^2}}}{2}\\ \Rightarrow {S_{BIC}} = {S_{ABC{\rm{D}}}} - {S_{AIB}} - {S_{CI{\rm{D}}}} = \frac{{3{a^2}}}{2}\end{array}\)
Gọi \(M\) là trung điểm của \(AB\)
\(\begin{array}{l} \Rightarrow BM = \frac{1}{2}AB = a,CM = AD = 2a \Rightarrow BC = \sqrt {B{M^2} + C{M^2}} = a\sqrt 5 \\ \Rightarrow IH = \frac{{2{{\rm{S}}_{BIC}}}}{{BC}} = \frac{{3a\sqrt 5 }}{5} \Rightarrow SI = IH.\tan \widehat {SHI} = \frac{{3a\sqrt {15} }}{5}\end{array}\)
\({V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SI = \frac{{3{a^3}\sqrt {15} }}{5}\)

Đáp án C
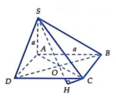
Gọi H là hình chiếu của C trên SO(O = AC ∩ BD), vì góc SOC tù nên H nằm ngoài SO
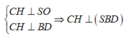
=> Góc tạo bởi SC và (SBD) là C S O ^
Ta có ![]()
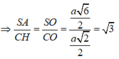
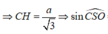
![]()

a/ Ta có: \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\)
Mà \(BD\perp AC\) (hai đường chéo hình thoi)
\(\Rightarrow BD\perp\left(SAC\right)\)
c/ Do \(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(\widehat{ABC}=60^0\Rightarrow\Delta ABC\) đều \(\Rightarrow AC=a\)
\(tan\widehat{SCA}=\frac{SA}{AC}=\frac{a\sqrt{3}}{a}=\sqrt{3}\)
\(\Rightarrow\widehat{SCA}=60^0\)

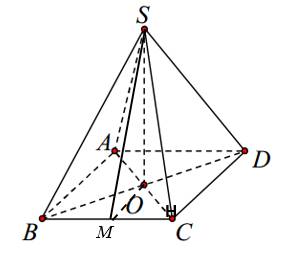
Gọi \(M\) là trung điểm \(BC\).
Ta có:\(OM=\dfrac{1}{2}.AB=2a;AC=\sqrt{AB^2+BC^2}=5a;OC=\dfrac{1}{2}AC=\dfrac{5}{2}a\)
\(SO=\sqrt{SC^2-OC^2}=\dfrac{5\sqrt{3}}{2}a\)
\(\left[S,BC,A\right]=\widehat{SMO}\)
\(\tan\widehat{SMO}=\dfrac{SO}{OM}=\dfrac{5\sqrt{3}}{4}\)
Suy ra:\(\widehat{SMO}=65,2^o\)
\(\Rightarrow D\)

Đáp án A.
Gọi H là hình chiếu của C trên SO và góc S O C ^ tù nên H nằm ngoài đoạn SO => CH ⊥ (SBD)
=> Góc tạo bởi SC và (SBD) là C S O ^
Lại có ![]()
![]()
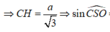
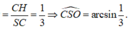

a. Ta có : \(\begin{cases}AB\perp BC\left(ABCDvuong\right)\\SA\perp BC\left(SA\perp\left(ABCD\right)\right)\end{cases}\) \(\Rightarrow BC\perp\left(SAB\right)\) mà \(SB\subset\left(SAB\right)\) nên \(BC\perp SB\) Vậy \(\Delta SBC\left(\perp B\right)\)
tương tự ta có : \(\begin{cases}SA\perp DC\\AD\perp DC\end{cases}\) \(\Rightarrow DC\perp\left(SAD\right)\) mà \(SD\subset\left(SAD\right)\) nên \(SD\perp DC\) Vậy \(\Delta SDC\left(\perp D\right)\)
ta có \(SA\perp AD\) nên \(\Delta SAD\left(\perp A\right)\)
Có \(SA\perp AB\) nên \(\Delta SAB\left(\perp A\right)\)
b. Ta có : \(\begin{cases}AC\perp BD\\SA\perp BD\end{cases}\) \(\Rightarrow BD\perp\left(SAC\right)\) mà \(BD\subset\left(SBD\right)\) nên \(\left(SAC\right)\perp\left(SBD\right)\)

Đáp án A.
Ta có: ![]() (chiều cao của hình chóp)
(chiều cao của hình chóp)
Diện tích hình vuông ![]()
Thể tích khối chóp SABCD là: 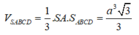
\(SA \bot \left( {ABCD} \right) \Rightarrow \left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
\(ABCD\) là hình vuông \( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = b\sqrt 2 \)
\(\cos \widehat {SCA} = \frac{{AC}}{{SC}} = \frac{1}{2} \Rightarrow \widehat {SCA} = {60^ \circ }\)
Vậy \(\left( {SC,\left( {ABCD} \right)} \right) = {60^ \circ }\)
Chọn A.