Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

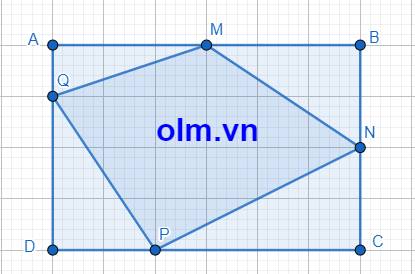
AQ = AD - DQ = AD - \(\dfrac{3}{4}\)AD = \(\dfrac{1}{4}\)AD
SAMQ = \(\dfrac{1}{2}\)AM\(\times\)AQ = \(\dfrac{1}{2}\times\)\(\dfrac{1}{2}\)AB\(\times\)\(\dfrac{1}{4}\)AD = \(\dfrac{1}{16}\)SABCD
SBMN = \(\dfrac{1}{2}\)MB\(\times\)BN = \(\dfrac{1}{2}\)\(\times\) \(\dfrac{1}{2}\)AB\(\times\)\(\dfrac{1}{2}\)BC = \(\dfrac{1}{8}\)SABCD
SCMN = \(\dfrac{1}{2}\)CN\(\times\)CP = \(\dfrac{1}{2}\times\dfrac{1}{2}\)BC \(\times\) \(\dfrac{2}{3}\)CD = \(\dfrac{1}{6}\)SABCD
DP = DC - CP = DC - \(\dfrac{2}{3}\)DC = \(\dfrac{1}{3}\)DC
SDPQ = \(\dfrac{1}{2}\times\)\(\dfrac{1}{3}\times\)DC \(\times\) \(\dfrac{3}{4}\)AD = \(\dfrac{1}{8}\)SABCD
Diện tích của tứ giác MNPQ là:
288 \(\times\)( 1 - \(\dfrac{1}{16}\) - \(\dfrac{1}{8}-\dfrac{1}{6}-\dfrac{1}{8}\)) = 150 (cm2)
ĐS...

Ta có: SAMP = 1212x AM x AP = 1212x (3434x AB) x (1212 x AD) = (1212 x3434 x 1212) x AB x AD = 316316x SABCD = 316316 x 192 = 36 cm2
SDPQ = 1212 x PD x DQ = 1212 x (1212x AD) x (1212x DC) = 1818x AD x DC = 1818x SABCD = 1818x 192 = 24 cm2
Tương tự, SNCQ = 320320x SABCD = 28,8 cm2 ; SBMN = 120120x SABCD = 9,6 cm2
=> SMNPQ = SABCD - ( SAMP + SDPQ + SNCQ + SBMN ) = 192 - (36 + 24 + 28,8 + 9,6) = 93,6 cm2
Vậy....

SQAM = SQDP = \(\dfrac{1}{6}\) SABCD = 48 cm2
SMBN = SPNC = \(\dfrac{1}{12}\) SABCD = 24 cm2
Diện tích hình MNPQ là:
288 - (48 + 24) x 2 = 144 (cm2)
Đáp số: 144 cm2
Kẻ 2 đường chéo của MNPQ lần lượt là MP; NQ
Vì AM =2/3 AB => MB = 1/3AB
=> Vì AB = DC => 1/3 AB = 1/3CD => MB = CP
=> Kẻ đường chéo thứ nhất từ M xuống C = Chiều rộng của hcn ABCD
Vì AM =2/3 AB => MB = 1/3AB
=> Vì AB = DC => 1/3 AB = 1/3CD => MB = CP
=> Kẻ đường chéo thứ nhất từ M xuống C = Chiều rộng của hcn ABCD
Vì AM =2/3 AB => MB = 1/3AB
=> Vì AB = DC => 1/3 AB = 1/3CD => MB = CP
=> Kẻ đường chéo thứ nhất từ M xuống C = Chiều rộng của hcn ABCD
Vì BN = NC ; DQ = QA
=> Vì BC =AD=> BN = NC = DQ = QA
=> Kẻ đường chéo thứ 2 từ N sang Q = Chiều dài của hcn ABCD
=> SMNPQ = NQ*MP : 2
Mà NQ = AB và MP = BC
=> SMNPQ = AB* BC : 2
Mà AB*BC= 288
=> SMNPQ = 288 : 2
SMNPQ = 144 (cm2)

Kiến thức mình còn kém nên không biết làm, nhờ các cậu giúp cho !
Đề của mình được trích từ Đề thi thử vào lớp 6, năm 2014 !
A B C D M N P Q
Nối B với D; B với P
Ta có SBPC = \(\frac{2}{3}\)SBDC (chung chiều cao hạ từ đỉnh B xuống CD; đáy CP = \(\frac{2}{3}\) CD )
SNPC = \(\frac{2}{3}\)SBPC (chung chiều cao hạ từ đỉnh P xuống BC; đáy NC = \(\frac{2}{3}\) CB)
=> SNPC = \(\frac{2}{3}\) x \(\frac{2}{3}\)SBDC = \(\frac{4}{9}\)SBDC = \(\frac{4}{9}\)x \(\frac{1}{2}\) SABCD = \(\frac{2}{9}\)SABCD
Tương tự; SBMN = \(\frac{1}{24}\)SABCD; SAMQ = \(\frac{9}{32}\)SABCD; SDPQ = \(\frac{1}{24}\) SABCD
vậy SNPC + SBMN + SAMQ + SDPQ = \(\left(\frac{2}{9}+\frac{1}{24}+\frac{9}{32}+\frac{1}{24}\right)\)SABCD = \(\frac{169}{288}\)SABCD = \(\frac{169}{288}\). 1152 = 676
=> S MNPQ = 1152 - 676 = 476 cm vuông
Cho hình chữ nhật ABCD có diện tích 216 cm2. Trên các cạnh AB, BC, CD và DA lần lượt lấy các điểm M, N, P, Q sao cho AM = MB, BN = 2/3 BC, CP = 2/3 CD và DQ = QA. Tính diện tích hình MNPQ?
dựa vào gợi ý trên đẻ làm nhé