Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

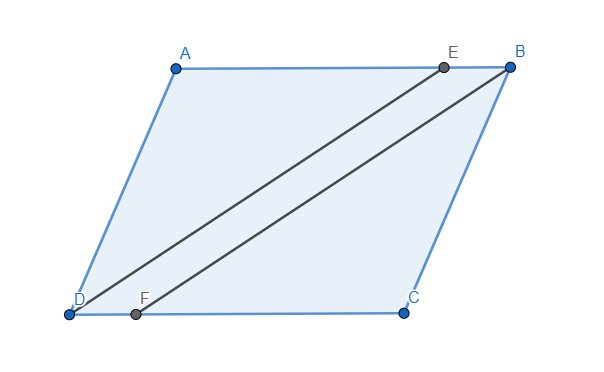
a) Ta thấy \(\widehat{AED}=\widehat{EDC}=\widehat{ADE}\) nên tam giác ADE cân tại A. Hoàn toàn tương tự thì tam giác CBF cân tại C.
Mặt khác, do tứ giác ABCD là hình bình hành nên \(\widehat{A}=\widehat{C},\widehat{B}=\widehat{D}\). Do đó \(\dfrac{\widehat{B}}{2}=\dfrac{\widehat{D}}{2}\) hay \(\widehat{CBF}=\widehat{ADE}\). Kết hợp với \(\widehat{A}=\widehat{C}\) thì suy ra \(\Delta ADE~\Delta CBF\left(g.g\right)\). Lại có \(\dfrac{AD}{CB}=1\) (do tứ giác ABCD là hình bình hành), suy ra \(\Delta ADE=\Delta CBF\) (2 tam giác đồng dạng có tỉ số đồng dạng bằng 1 thì 2 tam giác đó bằng nhau), ta có đpcm.
b) Ta thấy \(\widehat{AED}=\widehat{ADE}=\widehat{CBF}=\widehat{ABF}\) nên DE//BF. Lại có BE//DF (do tứ giác ABCD là hình bình hành) nên tứ giác DEBF cũng là hình bình hành (các cặp cạnh đối song song).
A B C D E F
a/
Xét tg ADE có
\(\widehat{ADE}=\widehat{CDE}\) (gt) (1)
\(\widehat{AED}=\widehat{CDE}\) (góc so le trong) (1)
Từ (1) và (2) => \(\widehat{ADE}=\widehat{AED}\) => tg ADE là tg cân tại A
=> AD=AE (3)
Xét tg CBF có
\(\widehat{CBF}=\widehat{ABF}\) (gt) (4)
\(\widehat{CFB}=\widehat{ABF}\) (góc so le trong) (5)
Từ (4) và (5) => \(\widehat{CBF}=\widehat{CFB}\) => tg CBF cân tại C
=> CB=CF (6)
Ta có
AD=CB (cạnh đối hình bình hành) (7)
Từ (3) (6) (7) => AD=AE=CB=CF
Mà \(\widehat{DAE}=\widehat{BCF}\) (góc đối hình bình hành)
=> tg ADE = tg CBF (c.g.c)
=> tg ADE và tg CBF là những tg cân bằng nhau
b/
tg ADE = tg CBF (cmt) \(\Rightarrow\widehat{BFC}=\widehat{ADE}\)
Mà \(\widehat{EDC}=\widehat{ADE}\) (gt)
\(\Rightarrow\widehat{BFC}=\widehat{EDC}\) Hai góc này ở vị trí đồng vị => DE//BF (8)
Ta có
AB//CD (cạnh đối hình bình hành) => BE//DF (9)
Từ (8) (9) => DEBF là hình bình hành (tứ giác có các cặp cạnh đối // với nhau là hình bình hành)

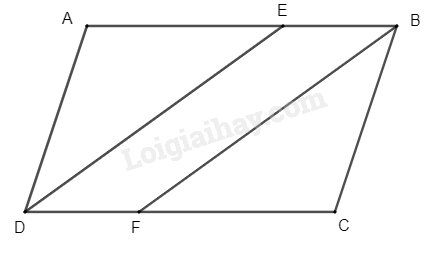
a) Vì \(DE\), \(BF\) là phân giác (gt)
Suy ra \(\widehat {{\rm{ADE}}} = \widehat {{\rm{EDC}}} = \frac{{\widehat {ADC}}}{2}\); \(\widehat {{\rm{EBF}}} = \widehat {{\rm{CBF}}} = \frac{{\widehat {ABC}}}{2}\) (1)
Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AB\) // \(CD\) và \(\widehat {ADC} = \widehat {ABC}\) (2)
Suy ra \(\widehat {{\rm{AED}}} = \widehat {{\rm{EDC}}}\) (so le trong) (3)
Từ (1), (2), (3) suy ra \(\widehat {AED} = \widehat {ABF}\)
Mà hai góc ở vị trí đồng vị
Suy ra \(DE\) // \(BF\)
b) Xét tứ giác \(DEBF\) ta có:
\(DE\) // \(BF\) (cmt)
\(BE\) // \(DF\) (do \(AB\) // \(CD\))
Suy ra \(DEBF\) là hình bình hành

\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\)\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\)

bạn vẽ hình nhé
a) ta có ABCD là hbh nên góc D = góc B
=> góc EDF = 1/2 góc D = 1/ góc B = góc EBF
ta lại có: góc EBF bù góc BFD (là hai góc trong cùng phía của hai đường thẳng // - AB//DC)
nên góc EDF cũng bù với góc BFD suy ra DE // DF ( có hai góc trong cùng phia bù nhau)
b) xét tư giác DEBF có
BE// DF (gt)
DE// BF (cmt)
vậy DEBF là hình bình hành

Bài 2:
AK=AB/2
CI=CD/2
mà AB=CD
nên AK=CI
Xét tứ giác AKCI có
AK//CI
AK=CI
Do đó: AKCI là hình bình hành
=>AC cắt KI tại trung điểm của mỗi đường(1)
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra AC,KI,BD đồng quy
Bài 1:
a: \(\widehat{ADE}=\widehat{EDF}=\dfrac{1}{2}\cdot\widehat{ADC}\)
\(\widehat{ABF}=\widehat{CBF}=\dfrac{1}{2}\cdot\widehat{ABC}\)
mà \(\widehat{ADC}=\widehat{ABC}\)
nên \(\widehat{ADE}=\widehat{EDF}=\widehat{ABF}=\widehat{CBF}\)
Xét ΔEAD và ΔFCB có
\(\widehat{A}=\widehat{C}\)
AD=CB
\(\widehat{EDA}=\widehat{FBC}\)
Do đó: ΔEAD=ΔFCB
=>\(\widehat{AED}=\widehat{CFB}\)
=>\(\widehat{EDF}=\widehat{CFB}\)
mà hai góc này đồng vị
nên DE//BF
b: Xét tứ giác DEBF có
DE//BF
BE//DF
Do đó: DEBF là hình bình hành

a: Ta có: \(\widehat{ADE}=\dfrac{\widehat{ADC}}{2}\)
\(\widehat{CBF}=\dfrac{\widehat{CBA}}{2}\)
mà \(\widehat{ADC}=\widehat{CBA}\)
nên \(\widehat{ADE}=\widehat{CBF}\)
Xét ΔADE và ΔCBF có
\(\widehat{ADE}=\widehat{CBF}\)
AD=BC
\(\widehat{DAE}=\widehat{BCF}\)
Do đó: ΔADE=ΔCBF
Suy ra: AE=CF
Ta có: AE+EB=AB
CF+DF=CD
mà AB=CD
và AE=CF
nên EB=DF
Xét tứ giác DEBF có
EB//DF
EB=DF
Do đó: DEBF là hình bình hành
Suy ra: DE//BF
d: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
e: Ta có: ABCD là hình bình hành
nên Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường\(\left(1\right)\)
Ta có: EBFD là hình bình hành
nên Hai đường chéo EF và BD cắt nhau tại trung điểm của mỗi đường\(\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra AC,BD,EF đồng quy