Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác DEBF có
BE//DF
BE=DF
Do đó: DEBF là hình bình hành
b: Vì DEBFlà hình bình hành
nên DB cắt EF tại trung điểm của mỗi đường(1)
Vì ABCD là hình bình hành
nên AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1), (2) suy ra E,O,F thẳng hàng
c: Để DEBF là hình thoi thì DE=BE=AB/2
Xét ΔDAB có
DE là trung tuyến
DE=AB/2
Do đo:ΔDAB vuông tại D
=>DA vuông góc với DB

a: Xét tứ giác DEBF có
BE//DF
BE=DF
Do đó: DEBF là hình bình hành
b: ta có: DEBF là hình bình hành
nên Hai đường chéo DB và EF cắt nhau tại trung điểm của mỗi đường(1)
Ta có:ABCD là hình bình hành
nên hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra BD,EF,AC đồng quy

a, Ta có:ABCD la hình bình hành=>AB=CD;AB//CD
mà E là trung diểm của AB;Flà trung điểm của CD
=>AE=EB=CF=DF(1)
VÌ AB//CD=>EB//DF(2)
Từ(1) và (2)=> EBFD là hình bình hành( theo dấu hiệu nhận biết hình bình hành)(đpcm)
b, Xét hbh ABCD có
AC cắt BD tại trung diểm củaAC và BD(1)
Xét hbh EBFD có EF cắt BD tại trung điểm của EF và BD(2)
từ (1) và (2)=>ba dường thang AC,BD,EF đồng quy
c,GỌI GIAO DIỂM CỦA AC,BD,EF LÀ O
Xét tam giác EOM và tam giác NOF có
góc EOM=góc NOF( đói đỉnh)
OE=OF(vi O là trung điểm cua EF)
goc MEF=góc NFE(vì CE//BF)
=>TAM GIAC EOM=TAMGIAC NOF
=.ME=NF(1)
TA CÓ ME//FN(2)
TU (1) VA(2)=>ENFM LA HBH

a) * Vì ABCD là hình bình hành(gt)
=> \(\widehat{A}=\widehat{C}\); \(\widehat{B}=\widehat{D};AD=BC;AB//CD\)( tính chất)
_ Ta có AM là tia phân giác của GÓC A => \(\widehat{A_1}=\widehat{A_2}=\frac{\widehat{A}}{2}\left(1\right)\)
_Ta có CN là tia phân giác của GÓC C =>\(\widehat{C_1}=\widehat{C_2}=\frac{\widehat{C}}{2}\left(2\right)\)
_ Từ (1) (2) => \(\widehat{A_1}=\widehat{C_2}\)
* Xét \(\Delta ADM\) và \(\Delta CBN\)có:
\(\widehat{A_1}=\widehat{C_2}\)( cmt)
AD=BC( cmt)
GÓC B=GÓC D
=> \(\Delta ADM=\Delta CBN\left(g.c.g\right)\)
=>AM=CN (3) ( 2 cạnh tuiwng ứng)
\(\widehat{M_1}=\widehat{N_1}\) ( 2 góc tương ứng)
* Mà AB//CD( gt)
\(N\in AB;M\in CD\left(gt\right)\)
=>BN//CM => \(\widehat{N_1}=\widehat{C_1}\)( 2 góc SLT)
=> \(\widehat{M_1}=\widehat{C_1}\)
Mà 2 góc này ở vị trí Đồng vị
=> AM//CN(4)
* Từ (3)(4)
=> AMCN là hình bình hành
_ Cậu tự vẽ hình xong đặt chỉ số ạ_
_tham khảo bài àm trên đây ạ, chúc cậu học tốt '.'

Bài 2:
AK=AB/2
CI=CD/2
mà AB=CD
nên AK=CI
Xét tứ giác AKCI có
AK//CI
AK=CI
Do đó: AKCI là hình bình hành
=>AC cắt KI tại trung điểm của mỗi đường(1)
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra AC,KI,BD đồng quy
Bài 1:
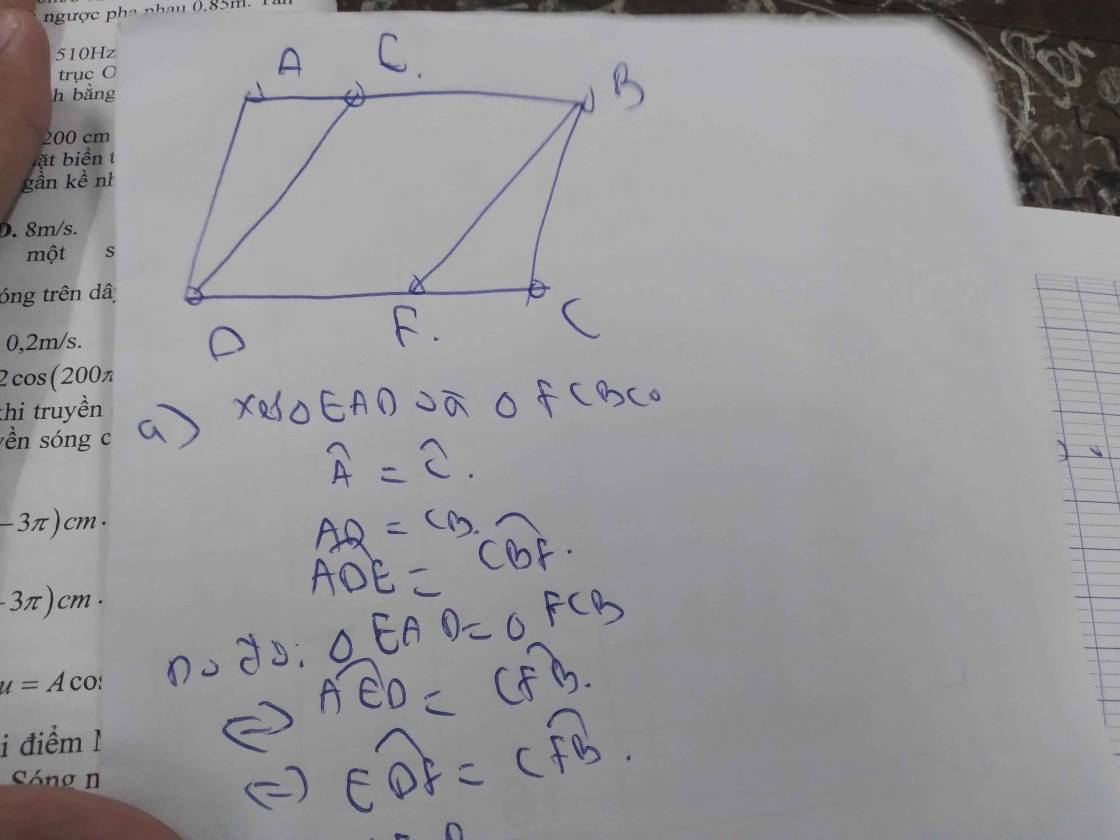
a: \(\widehat{ADE}=\widehat{EDF}=\dfrac{1}{2}\cdot\widehat{ADC}\)
\(\widehat{ABF}=\widehat{CBF}=\dfrac{1}{2}\cdot\widehat{ABC}\)
mà \(\widehat{ADC}=\widehat{ABC}\)
nên \(\widehat{ADE}=\widehat{EDF}=\widehat{ABF}=\widehat{CBF}\)
Xét ΔEAD và ΔFCB có
\(\widehat{A}=\widehat{C}\)
AD=CB
\(\widehat{EDA}=\widehat{FBC}\)
Do đó: ΔEAD=ΔFCB
=>\(\widehat{AED}=\widehat{CFB}\)
=>\(\widehat{EDF}=\widehat{CFB}\)
mà hai góc này đồng vị
nên DE//BF
b: Xét tứ giác DEBF có
DE//BF
BE//DF
Do đó: DEBF là hình bình hành