Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x^2=1^2+1^2\left(pythagore\right)\\ \Rightarrow x=\sqrt{2}\\ \sqrt{5}^2=1^2+y^2\left(pythagore\right)\\ \Rightarrow y=\sqrt{4}=2\)
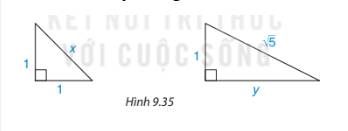
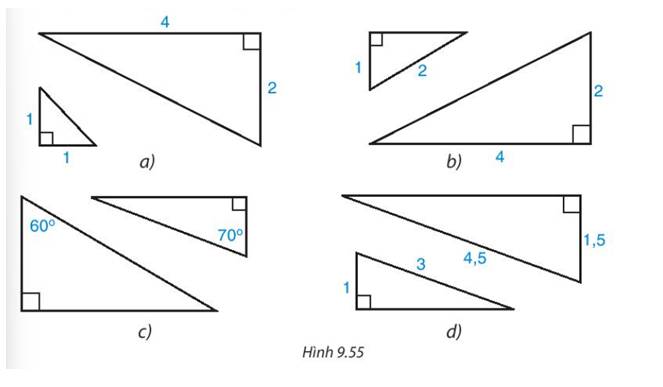
a) \(x^2=1^2+1^2=2\Rightarrow x=\sqrt[]{2}\)
b) \(\left(\sqrt[]{5}\right)^2=y^2+1^2\Rightarrow y^2=5-1=4\Rightarrow y=2\)

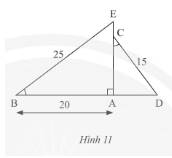
Xét \(\Delta ABE\) và \(\Delta ACD\) có:
\(\widehat {EBA} = \widehat {ACD}\) (giả thuyết)
\(\widehat {BAE} = \widehat {CAD} = 90^\circ \)
Do đó, \(\Delta ABE\backsim\Delta ACD\) (g.g)
Vì \(\Delta ABE\backsim\Delta ACD\) nên \(\frac{{AB}}{{AC}} = \frac{{EB}}{{CD}}\) (các cặp cạnh tương ứng)
Thay số, \(\frac{{20}}{{AC}} = \frac{{25}}{{15}} \Rightarrow AC = \frac{{20.15}}{{25}} = 12\)cm.
Áp dụng định lí Py – ta – go cho \(\Delta ABE\) vuông tại \(A\) ta có:
\(B{E^2} = A{E^2} + A{B^2} \Leftrightarrow A{E^2} = B{E^2} - A{B^2} = {25^2} - {20^2} = 225 \Rightarrow AE = \sqrt {225} = 15\)cm.
Độ dài \(CE\) là:
15 – 12 = 3cm
Vậy \(CE = 3cm.\)

Cặp tam giác vuông ở hình d. Vì cạnh huyền và một cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia

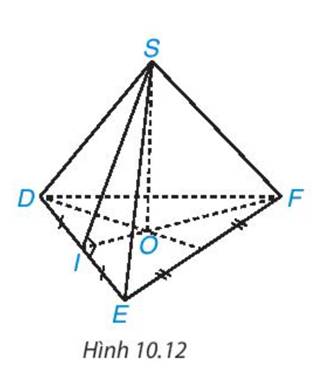
- Đỉnh: S
- Cạnh bên: SD, SE, SF
- Mặt bên: SDE, SEF, SDF
- Mặt đáy: DEF
- Đường cao: SO
- Một trung đoạn: SI

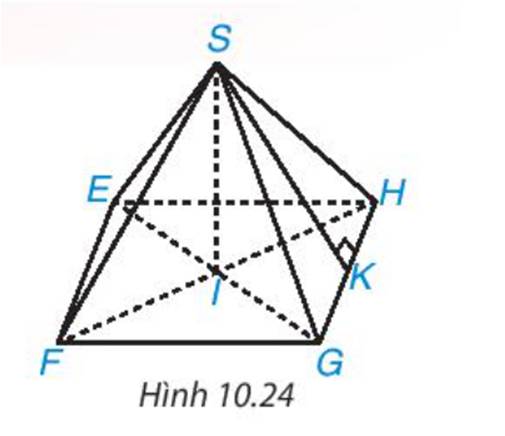
- Đỉnh: S
- Cạnh bên: SE, SF, SG, SH
- Mặt bên: SEF, SFG, SGH. SEH
- Mặt đáy: EFGH
- Đường cao: SI
- Một trung đoạn: SK

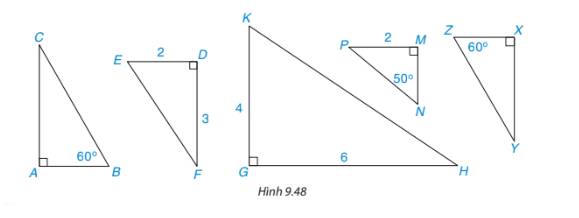
Các cặp tam giác vuông đồng dạng:
\(\begin{array}{l}\Delta ABC \backsim \Delta X{\rm{Z}}Y(\widehat A = \widehat X;\widehat B = \widehat Z)\\\Delta E{\rm{D}}F \backsim \Delta KGH\left( {\frac{{E{\rm{D}}}}{{KG}} = \frac{{DF}}{{GF}};\widehat {E{\rm{D}}F} = \widehat {KGH}} \right)\end{array}\)

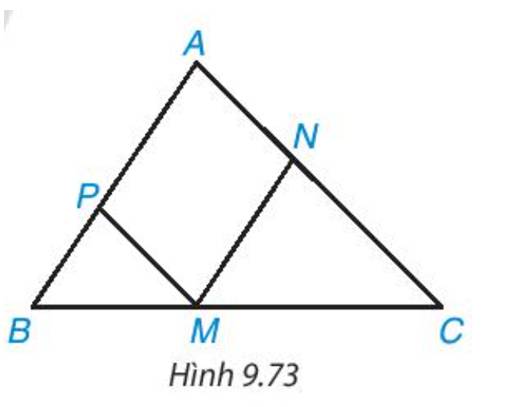
- ΔCNM ~ ΔCAB (vì MN // AB) (1)
- ΔMPB ~ ΔCAB (vì MP // AC) (2)
- Từ (1) và (2) => ΔCNM ~ ΔMPB

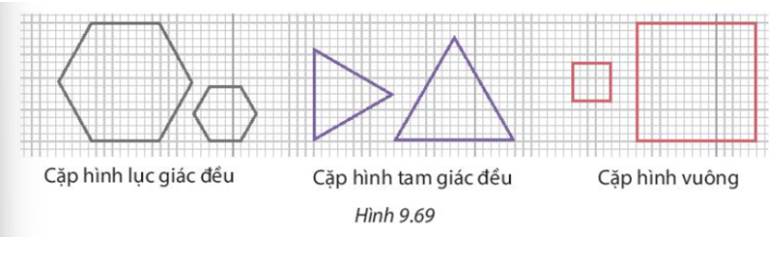
Cặp hình lục giác đều và cặp hình vuông là đồng dạng phối cảnh
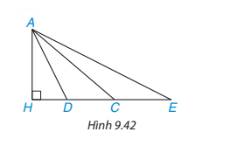
Áp dụng định lí Pythagore trong tam giác AHD vuông tại H có: \(A{{\rm{D}}^2} = A{H^2} + H{{\rm{D}}^2}\) (1)
Áp dụng định lí Pythagore trong tam giác AHC vuông tại H có: \(A{C^2} = A{H^2} + H{C^2}\) (2)
Áp dụng định lí Pythagore trong tam giác AHE vuông tại H có: \(A{E^2} = A{H^2} + H{E^2}\) (3)
Vì HE > HC > HD suy ra \(H{E^2} > H{C^2} > H{{\rm{D}}^2}\)(4)
Từ (1), (2), (3), (4) suy ra: \(A{{\rm{E}}^2} > A{C^2} > A{{\rm{D}}^2} \Rightarrow A{\rm{E}} > AC > A{\rm{D}}\)
Vậy đoạn AE là lớn nhất, đoạn AD là nhỏ nhất.