Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

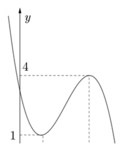
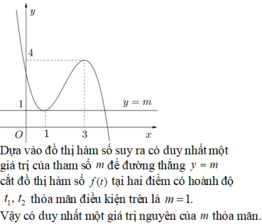
Đặt \(f\left(x\right)=t\Rightarrow t^3-3t+2=m\)
- Với \(\left[{}\begin{matrix}m< 0\\m>4\end{matrix}\right.\) pt có nghiệm duy nhất
- Với \(0< m< 4\) pt có 3 nghiệm pb
- Với \(\left[{}\begin{matrix}m=0\\m=4\end{matrix}\right.\) pt có 2 nghiệm pb
Xét pt \(f\left(x\right)=t\Leftrightarrow x^7+x^5-x^4+x^3-2x^2+2x-10=t\)
Ta có \(f'\left(x\right)=7x^6+5x^4-4x^3+3x^2-4x+2\)
\(=7\left(x^3-\frac{2}{7}\right)^2+5x^4+3\left(x-\frac{2}{3}\right)^2+\frac{2}{21}>0\)
\(\Rightarrow f\left(x\right)\) đồng biến \(\Rightarrow f\left(x\right)=t\) có nghiệm duy nhất
\(\Rightarrow\) Để pt có 3 nghiệm pb thì \(0< m< 4\)

\(g'\left(x\right)=\left(2x-8\right)f'\left(x^2-8x+m\right)\)
Ta không cần quan tâm tới nhân tử \(\left(x-1\right)^2\) ở \(f'\left(x\right)\) vì đó là biểu thức mũ chẵn nên ko làm \(f'\left(x\right)\) đổi dấu khi đi qua \(x=1\)
\(g'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}2x-8=0\Rightarrow x=4\\\left(x^2-8x+m\right)^2-2\left(x^2-8x+m\right)=0\left(1\right)\end{matrix}\right.\)
Để hàm số đồng biến trên \(\left(4;+\infty\right)\Rightarrow\left(1\right)\) vô nghiệm hoặc tất cả các nghiệm của (1) đều không lớn hơn 4
\(\left(1\right)\Leftrightarrow\left(x^2-8x+m\right)\left(x^2-8x+m-2\right)=0\)
TH1: \(16-m+2\le0\Rightarrow m\ge18\)
TH2: Nhận thấy 2 pt \(\left\{{}\begin{matrix}x^2-8x+m=0\\x^2-8m+m-2=0\end{matrix}\right.\)
Đều có trung bình cộng hai nghiệm \(\frac{x_1+x_2}{2}=4\Rightarrow\) nếu 2 pt này có nghiệm thì luôn có ít nhất 1 nghiệm lớn hơn 4 \(\Rightarrow\) ko thỏa mãn
Vậy \(m\ge18\) \(\Rightarrow\) có \(99-18+1=82\) giá trị nguyên của m

\(g'\left(x\right)=-f'\left(3-x\right)=\left(x-3\right)\left(2-x\right)^2\left(\left(3-x\right)^2+9\left(3-x\right)+9\right)\)
Không cần quan tâm tới \(\left(2-x\right)^2\) do \(g'\left(x\right)\) ko đổi dấu khi đi qua điểm dừng này
\(g'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=3\\\left(3-x\right)^2+m\left(3-x\right)+9=0\left(1\right)\end{matrix}\right.\)
Để \(g\left(x\right)\) đồng biến trên \(\left(3;+\infty\right)\Rightarrow\left(1\right)\) vô nghiệm hoặc các nghiệm của (1) đều không lớn hơn 3
\(\left(1\right)\Leftrightarrow h\left(x\right)=x^2-\left(m+6\right)x+3m+18=0\)
\(\Delta=m^2-36\)
TH1: \(\Delta< 0\Rightarrow m^2-36< 0\Rightarrow-6< m< 6\)
TH2: \(\left\{{}\begin{matrix}\Delta\ge0\\h\left(3\right)>0\\\frac{m+6}{2}< 3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m\ge6\\m\le-6\end{matrix}\right.\\9>0\\m< 0\end{matrix}\right.\) \(\Rightarrow m\le-6\)
Vậy \(m< 6\) thì \(g\left(x\right)\) đồng biến trên \(\left(3;+\infty\right)\Rightarrow\) có 5 giá trị nguyên dương

Chọn \(f\left(x\right)=x^3+ax^2+bx+c\)
\(2f\left(x^2\right)+f'\left(x\right)=2x^6+7x^2+2\)
\(\Leftrightarrow2x^6+2ax^4+2bx^2+c+3x^2+2ax+b=2x^6+7x^2+2\)
\(\Leftrightarrow2ax^4+\left(2b+3\right)x^2+2ax+b+c=7x^2+2\)
Đồng nhất 2 vế ta được: \(\left\{{}\begin{matrix}a=0\\2b+3=7\\b+c=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=c=0\\b=2\end{matrix}\right.\)
\(\Rightarrow f\left(x\right)=x^3+2x\Rightarrow f\left(1\right)=3\)

\(y'=\frac{5\left(x^2+4\right)-2x.5x}{\left(x^2+4\right)}f'\left(\frac{5x}{x^2+4}\right)=\frac{5\left(4-x^2\right)}{x^2+4}f'\left(\frac{5x}{x^2+4}\right)\)
\(=\frac{5\left(2-x\right)\left(2+x\right)}{\left(x^2+4\right)}.\left(\frac{5x}{x^2+4}\right)^2.\left(\frac{5x}{x^2+4}-1\right)\left(\frac{65x}{x^2+4}-15\right)^3\)
\(=\frac{5\left(2-x\right)\left(2+x\right).25x^2\left(x-4\right)\left(1-x\right)\left(x-3\right)^3\left(4-3x\right)^3.5^3}{\left(x^2+4\right)^7}\)
Ta thấy \(y'=0\) có 7 nghiệm nhưng nghiệm \(x=0\) có mũ chẵn nên hàm số có 6 điểm cực trị

Đơn giản là bạn vẽ cái hàm bậc 4 đó ra và cho -m và -m-10 cắt thôi. Vì -m-10<-m nên -m-10 sẽ nằm ở dưới, còn -m nằm trên. Nên -m sẽ cắt 2 điểm và -m-10 cắt 4 điểm cho ta 6 điểm. Ngoài ra k còn trường hợp nào khác mà -m và -m-10 cắt thỏa mãn

Câu 1:
\(\left(x+2\right)f\left(x\right)+x\left(x+1\right)f'\left(x\right)=x\left(x+1\right)\)
\(\Leftrightarrow x\left(x+2\right)f\left(x\right)+x^2\left(x+1\right)f'\left(x\right)=x^2\left(x+1\right)\)
\(\Leftrightarrow\frac{x\left(x+2\right)}{\left(x+1\right)^2}f\left(x\right)+\frac{x^2}{x+1}f'\left(x\right)=\frac{x^2}{x+1}\)
\(\Leftrightarrow\left(\frac{x^2}{x+1}f\left(x\right)\right)'=\frac{x^2}{x+1}=x-1+\frac{1}{x+1}\)
Lấy nguyên hàm 2 vế:
\(\Leftrightarrow\frac{x^2}{x+1}.f\left(x\right)=\frac{x^2}{2}-x+ln\left|x+1\right|+C\)
Thay \(x=1\Rightarrow ln2+\frac{1}{2}=\frac{1}{2}-1+ln2+C\Rightarrow C=1\)
\(\Rightarrow\frac{x^2}{x+1}f\left(x\right)=\frac{x^2}{2}-x+ln\left|x+1\right|+1\)
Thay \(x=2\Rightarrow\frac{4}{3}f\left(2\right)=ln3+1\Rightarrow f\left(2\right)=\frac{3}{4}ln+\frac{3}{4}\Rightarrow T=-\frac{3}{16}\)
Câu 2:
\(I_1=\int\limits^2_0f\left(x\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=x\end{matrix}\right.\)
\(\Rightarrow I_1=x.f\left(x\right)|^2_0-\int\limits^2_0x.f'\left(x\right)dx=2-\int\limits^2_0x.f'\left(x\right)dx\)
Mà \(I_1=2\)\(\Rightarrow I_2=\int\limits^2_0x.f'\left(x\right)dx=-2\)
Đặt \(2x=t\Rightarrow x=\frac{t}{2}\Rightarrow dx=\frac{1}{2}dt\) ; \(\left\{{}\begin{matrix}x=0\Rightarrow t=0\\x=2\Rightarrow t=4\end{matrix}\right.\)
\(\Rightarrow I_2=\int\limits^4_0\frac{t}{2}f'\left(\frac{t}{2}\right).\frac{1}{2}dt=\frac{1}{4}\int\limits^4_0t.f'\left(\frac{t}{2}\right)dt=-2\)
\(\Rightarrow\int\limits^4_0t.f'\left(\frac{t}{2}\right)dt=-8\) hay \(\int\limits^4_0x.f'\left(\frac{x}{2}\right)dx=-8\)

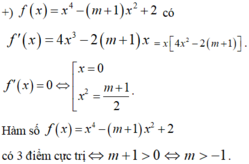
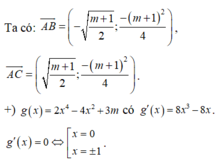

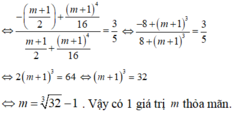

Chọn B