Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng

Chọn A
f ' ( x ) đổi dấu khi x chạy qua -1 và 3 nên hàm số có 2 điểm cực trị.

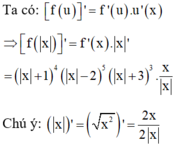
Do đó hàm số f(|x|) có 3 điểm cực trị tại x= 2; x= -2 và x= 0
Chọn B.

Đơn giản là bạn vẽ cái hàm bậc 4 đó ra và cho -m và -m-10 cắt thôi. Vì -m-10<-m nên -m-10 sẽ nằm ở dưới, còn -m nằm trên. Nên -m sẽ cắt 2 điểm và -m-10 cắt 4 điểm cho ta 6 điểm. Ngoài ra k còn trường hợp nào khác mà -m và -m-10 cắt thỏa mãn



\(y'=\frac{5\left(x^2+4\right)-2x.5x}{\left(x^2+4\right)}f'\left(\frac{5x}{x^2+4}\right)=\frac{5\left(4-x^2\right)}{x^2+4}f'\left(\frac{5x}{x^2+4}\right)\)
\(=\frac{5\left(2-x\right)\left(2+x\right)}{\left(x^2+4\right)}.\left(\frac{5x}{x^2+4}\right)^2.\left(\frac{5x}{x^2+4}-1\right)\left(\frac{65x}{x^2+4}-15\right)^3\)
\(=\frac{5\left(2-x\right)\left(2+x\right).25x^2\left(x-4\right)\left(1-x\right)\left(x-3\right)^3\left(4-3x\right)^3.5^3}{\left(x^2+4\right)^7}\)
Ta thấy \(y'=0\) có 7 nghiệm nhưng nghiệm \(x=0\) có mũ chẵn nên hàm số có 6 điểm cực trị