Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
\(y'=\frac{2}{3}x+m\geq 0, \forall x\in\mathbb{R}\Leftrightarrow m\geq -\frac{2}{3}x, \forall x\in\mathbb{R}\)
\(\Leftrightarrow m\geq \max (\frac{-2}{3}x), \forall x\in\mathbb{R}\)
Vì $\frac{-2}{3}x$ không có max với mọi $x\in\mathbb{R}$ nên không tồn tại $m$

1) \(y=\dfrac{2x^2+1}{x^2}\)
\(\Rightarrow y'=\dfrac{\left(4x+1\right)x^2-2x\left(2x^2+1\right)}{x^4}\)
\(\Leftrightarrow y'=\dfrac{4x^3+x^2-4x^3-2x}{x^4}\)
\(\Leftrightarrow y'=\dfrac{x^2-2x}{x^4}=\dfrac{x\left(x-2\right)}{x^4}=\dfrac{x-2}{x^3}\)
2) \(f\left(x\right)=\sqrt[]{-5x^2+14x-9}\)
\(\Rightarrow f'\left(x\right)=\dfrac{-10x+14}{2\sqrt[]{-5x^2+14x-9}}\)
\(\Leftrightarrow f'\left(x\right)=\dfrac{-2\left(5x-7\right)}{2\sqrt[]{-5x^2+14x-9}}\)
\(\Leftrightarrow f'\left(x\right)=\dfrac{-\left(5x-7\right)}{\sqrt[]{-5x^2+14x-9}}\)
Để \(f'\left(x\right)=0\)
\(f'\left(x\right)=\dfrac{-\left(5x-7\right)}{\sqrt[]{-5x^2+14x-9}}=0\)
\(\Leftrightarrow5x-7=0\)
\(\Leftrightarrow5x=7\)
\(\Leftrightarrow x=\dfrac{7}{5}\)
Vậy tập hợp giá trị để \(f'\left(x\right)=0\) là \(\left\{\dfrac{7}{5}\right\}\)

\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\sqrt{2x-4}+3\)
\(=\sqrt{2\cdot2-4}+3=3\)
\(f\left(2\right)=\sqrt{2\cdot2-4}+3=0+3=3\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\dfrac{x+2}{x^2-2mx+m^2+2}\)
\(=\dfrac{2+2}{2^2-2m\cdot2+m^2+2}=\dfrac{4}{m^2-4m+6}\)
Để hàm số f(x) liên tục trên R thì f(x) liên tục tại x=2
=>\(\dfrac{4}{m^2-4m+6}=3\)
=>\(4=3\left(m^2-4m+6\right)\)
=>\(3m^2-12m+18-4=0\)
=>\(3m^2-12m+14=0\)
\(\Leftrightarrow3m^2-12m+12+2=0\)
=>\(3\left(m-2\right)^2+2=0\)(vô lý)
=>\(m\in\varnothing\)

\(f\left(x\right)=-x^3-2x^2+mx-3\)
\(f'\left(x\right)=-3x^2-4x+m\)
\(f'\left(x\right)>0\Leftrightarrow-3x^2-4x+m>0\Leftrightarrow m>3x^2+4x\)(đúng với mọi \(x\in\left(0,1\right)\))
suy ra \(m\ge max\left(3x^2+4x\right)\)với \(x\in\left[0,1\right]\).
Xét hàm \(g\left(x\right)=3x^2+4x\)với \(x\in\left[0,1\right]\).
\(g'\left(x\right)=6x+4\)
\(g'\left(x\right)=0\Leftrightarrow6x+4=0\Leftrightarrow x=-\frac{2}{3}\notin\left[0,1\right]\).
\(g\left(0\right)=0,g\left(1\right)=7\)
suy ra \(g_{max}=7\)
do đó \(m\ge7\).
Mà \(m\)nguyên, \(m\in\left[-2021,2021\right]\)nên có tổng cộng: \(2021-7+1=2015\)giá trị của \(m\)thỏa mãn.

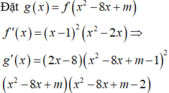
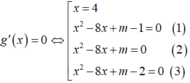


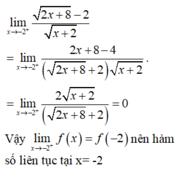
Để hàm số có đạo hàm tại x=0 phải thỏa mãn 2 điều kiện, đó là hàm số liên tục tại x=0 và có đạo hàm bên trái bằng đạo hàm bên phải
Để hàm số liên tục tại x=0 \(\Leftrightarrow\lim\limits_{x\rightarrow0^+}=\lim\limits_{x\rightarrow0^-}=f\left(0\right)\Leftrightarrow2=2\left(tm\right)\)
\(f'\left(0^+\right)=\lim\limits_{x\rightarrow0^+}\dfrac{f\left(x\right)-f\left(0\right)}{x-0}=\lim\limits_{x\rightarrow0^+}\dfrac{mx^2+2x+2-2}{x}=\lim\limits_{x\rightarrow0^+}\dfrac{x\left(mx+2\right)}{x}=2\)
\(f'\left(0^-\right)=\lim\limits_{x\rightarrow0^-}\dfrac{f\left(x\right)-f\left(0\right)}{x-0}=\lim\limits_{x\rightarrow0^-}\dfrac{nx+2-2}{x}=n\)
\(\Rightarrow\left\{{}\begin{matrix}m\in R\\n=2\end{matrix}\right.\)
\(f\left(0^+\right)=f\left(0^-\right)\Leftrightarrow n=2\)