Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) OD // CE (_|_ OE) và CD // OE (_|_OD)
=> ODCE là hình bình hành . Mà O^ = 90o
=> ODCE là hình chữ nhật (*) => CE=OD
b) (*) => DCE^ = 90o hay CE_|_ CD
c) tam giác ADC và tam giác CEB:
AD = CE (=DO)
EDC^ = CEB^ = 90o
DC=EB (=OE)
=> tam giác ADC= tam giác CEB (2 cạnh góc vuông)
=> AC = CB ( 2 cạnh tương ứng)
d) AD //= CE (cmt) => tứ giác ACED là hình bình hành => AC // DE (*)
e) DC //= EB => tứ giác DCBE là hình bình hành
=> DE//BC ( 2 cạnh đối) (**)
Từ (*) và (**) => A,C,B thẳng hàng

\(\left\{{}\begin{matrix}\overrightarrow{IJ}=\overrightarrow{IA}+\overrightarrow{AB}+\overrightarrow{BJ}\\\overrightarrow{IJ}=\overrightarrow{ID}+\overrightarrow{DC}+\overrightarrow{CJ}\end{matrix}\right.\)
Cộng vế với vế:
\(2\overrightarrow{IJ}=\left(\overrightarrow{IA}+\overrightarrow{ID}\right)+\left(\overrightarrow{BJ}+\overrightarrow{CJ}\right)+\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AB}+\overrightarrow{DC}\)
\(\Rightarrow\overrightarrow{IJ}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{DC}\)
b/ Đặt \(\frac{MA}{MB}=\frac{ND}{NC}=k\)
\(\left\{{}\begin{matrix}\overrightarrow{IP}=\overrightarrow{IA}+\overrightarrow{AM}+\overrightarrow{MP}\\\overrightarrow{IP}=\overrightarrow{ID}+\overrightarrow{DN}+\overrightarrow{NP}\end{matrix}\right.\)
\(\Rightarrow2\overrightarrow{IP}=\left(\overrightarrow{IA}+\overrightarrow{ID}\right)+\left(\overrightarrow{MP}+\overrightarrow{NP}\right)+\overrightarrow{AM}+\overrightarrow{DN}=\overrightarrow{AM}+\overrightarrow{DN}\)
\(\Rightarrow2\overrightarrow{IP}=k.\overrightarrow{AB}+k.\overrightarrow{DC}\)
\(\Rightarrow\overrightarrow{IP}=\frac{k}{2}\left(\overrightarrow{AB}+\overrightarrow{DC}\right)=\frac{k}{2}.\overrightarrow{IJ}\Rightarrow P;I;J\) thẳng hàng hay P thuộc IJ

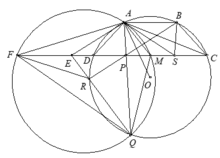
1). Gọi S điểm đối xứng với P qua M.Theo tính chất đối xứng của hình thang cân dễ thấy tứ giác ABSP cũng là hình thang cân.
Ta lại có Q P S ^ = Q A B ^ = Q R B ^ .
Từ đó có E P Q ^ = E R P ^ ⇒ Δ E R P ∽ Δ E P Q (g – g),
nên E Q P ^ = E P R ^ = B P S ^ = A S E ^ , suy ra tứ giác AEQS nội tiếp.
Do đó P A . P Q = P E . P S = P F 2 .2 P M = P F . P M , suy ra tứ giác A M Q F nội tiếp.
Từ đó suy ra đường tròn ngoại tiếp tam giác △ A Q F luôn đi qua M.